EXAMPLES ON GAS LAWS
Example1
A certain mass of an ideal gas has a volume of 3.25dm3 at 25oc and 1.01  105 NM -2 . What pressure is required to compress it to 1.88dm3 at the some temperature.
105 NM -2 . What pressure is required to compress it to 1.88dm3 at the some temperature.
Solution
V1 = 3.25dm
T1 = 25OC
P1 = 1.01  105 NM-2
105 NM-2
T2 = 250
P2 = ?
V2 = 1.88
So.
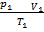 =
= 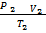
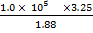 =
= 
Note:
P2 = 1.746 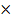 105NM-2
105NM-2
1.01 105NM-2 = 1atm
1.01 105NM-2 = 760 mmHg
1 NM-2 = 1 Pa
Example 2.
It takes 54.4 sec. for 100cm3 of a gas 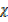 to effuse through an aperture and 36 . 5 sec for 100cm3 of O2 to effuse through the same aperture
to effuse through an aperture and 36 . 5 sec for 100cm3 of O2 to effuse through the same aperture
i) What is the molar mass of gas X
ii) Suggest the gas X
Solution
Rate

From Graham’s law
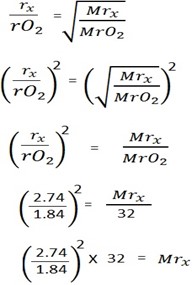
MrX = 70.9
MrX≈71
i) The molar mass of gas X is 71g/mol
ii) The gas X is chlorine gas
Example 3
a) Define the following terms
i. Effusion
ii) Critical temperature
b) State Grahm’s law of diffusion
A certain volume of hydrogen takes 2min and 10 sec to diffuse through a porous plug and an oxide of nitrogen takes 10min 223 sec.
What is:
i) Molar mass of an oxide
ii) Give the following of an oxide
Solution
V be the volume of hydrogen
V be the volume of oxide
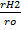 =
= 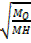
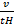
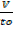 =
= 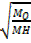
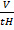

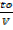 =
= 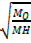

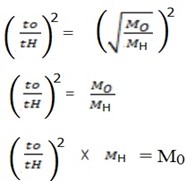
t0 = 623 sec MH = 2
tH = 130 sec
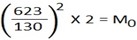
M0 = 46
i) The moles mass of the oxide is 46g/mol
ii) The formula of the oxide is NO2
iii) Effusion is the escaping of a gas through a porous without molecular collision between molecules of gas.
iv) Graham’s law of diffusion state that. At the same temperature and pressure the rate of diffusion of different is inversely proportional to the square roots their Mr mass.
v) Critical temperature is the temperature above which the gas cannot be liquefied without further cooling.
Example 4
a) State the kinetic theory of gases
b) Write down the equation of the gas which do obey all assumption in (a) above and define the terms
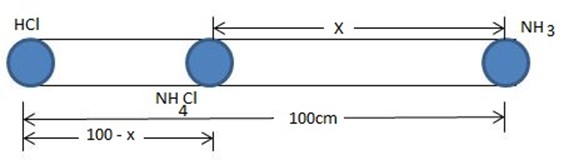
c) A plug of cotton wool one soaked in conc. Hcl where inserted into opposite ends of a horizontal glass tube
A disc of solid ammonium chloride formed in the tube plug is the 1m long how for from the ammonia plug is the deposited
Solution
Reaction
NH3 + Hcl  NH4
NH4
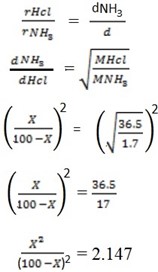
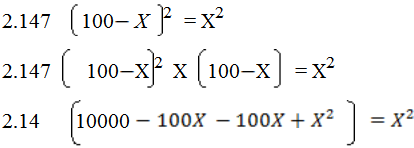
21407  429.4X + 2.147X2 = X2
429.4X + 2.147X2 = X2
2.147 X2 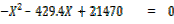
Solving quadratically
The solid deposit 59.4 cm away from N
a) The kinetic theory of gases states that
i) Molecules of a gas are far way such that force of attraction between the individual molecule is neglible
ii) The collision of gas molecules are perfectly elastic
iii) The pressure of a gas inside the container is due to the collision between the molecules of the gas and the wall of the container
iv) Gases container a large number of molecules which exist in continuous random motion
v) Kinetic energy of molecules is directly proportional to the absolute temperature
vi) The volume of individual molecules of the gas is negligible compared to the volume of the container.
b) Equation of the gases that obey kinetic theory of gases is as follows:
PV = nRT
Where by
P = Is the pressure of the gas
V = Is the volume of the gas
n = I s the number of molecules of the gas
R = is the universal constant
T = Is the absolute temperature
Example 5.
A) A certain volume of SO2 diffuses through a porous plug in 10.0 min and the same volume of second gas takes 15.8 min. Calculate the relative molecules mass of the second gas
B) Nicked from a carbonyl, Ni (CO) n Deduce the value of n from the fact that carbon monoxide diffuse 2.46 times faster than the carbon compound .
Solution
Let V be the volume of SO2
V be the volume of gas x (gx)
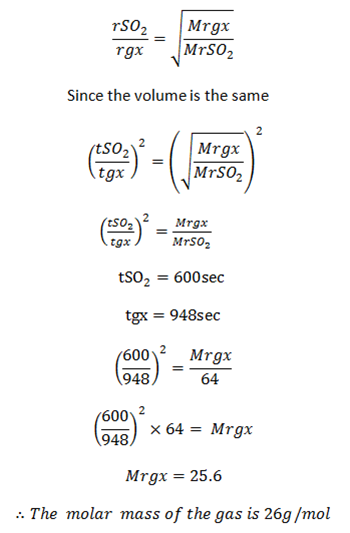
Solution
Mr of Ni (CO)n = 59 +(28)n
Mr of CO = 28
Let time takes for carbonyl to diffuse = x
Time taken for carbon monoxide to diffuse = 2.46x
From Graham’s law
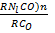 =
= 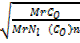
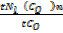 =
= 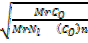
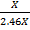 =
= 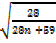
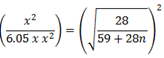
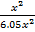 =
= 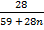
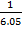 =
= 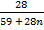
28 = 9.75 + 4.62n
0.165 = 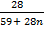
28 = 9.75 + 4.62n
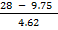 =
= 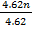
n = 3.9 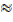 4
4
The volume of n in Nl (CO) is 4
MOLE FRACTION OF A GAS
Mole fraction of a gas is defined as the ratio of number of mass of such gas per total moles of gases present
The moles fraction is denoted by 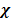 (
(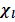 )
)
Example
If there are two gas ie. Gas A and gas B in the container. Show how can you find the mole fraction each gas
Solution
Gases present
Gas A and gas B
Let n
A be number of moles of gas A
nB be number of moles of gas B
nT = nA + nB
 =
= 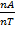
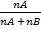
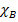 =
=  =
= 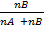
Note
When mole are expressed in % will sum up to 100%
And when expressed in decimal will not exceed 1.00
From the example above In %
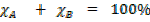
In decimals
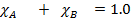
Ie 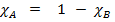
Example
The container was found to have 8g of oxygen and 4.4g of CO2. What is the percentage composition of O2 and CO2 in the container
Solution
Mass of oxygen = 8g
Mass of carbon dioxide = 4.4g
No of mole of O2 = 
= 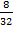
= 0.25
No of moles of CO2 = 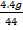
= 0.1
Total number of moles = 0.1 + 0.25
= 0.35
% composition of m moles = 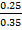
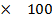
= 0.174 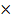 100
100
= 71.4%
% composition of CO2 = 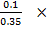 100
100
= 0.285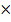 100
100
= 29%
The percentage of composition of O2 and CO2 in the container are 71.4% and 29%
Critical pressure is the pressure at which the gas starts to liquify
Example
A mixture of CO and CO2 diffusion through a porous diagram in on half of the time taken for the same volume of Bromine vapour. What is the composition by volume of the mixture?
Solution
Let time taken by Br2 be t
Time taken by the mixture CO + CO2 be 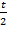
Volume I is common rate of mixture = 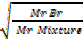 tare of Br2
tare of Br2
but
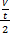 = rate for mixture
= rate for mixture
 = rate Br2
= rate Br2
Mr Br2 = 80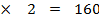
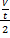

 =
= 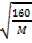

 2
2 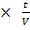 =
= 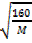
 =
= 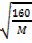
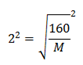
4 = 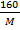
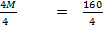
M = 40
Mr of CO = 28
Mr of CO2 = 44
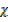 CO Mr
CO Mr 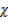 CO2
CO2 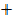 Mr CO2 = 40
Mr CO2 = 40
 CO
CO 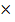 28 +
28 + 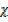 CO
CO 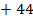 = 40
= 40
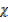 CO
CO 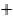
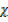 CO = 1
CO = 1
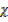 CO2 = 1
CO2 = 1 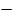
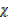 CO
CO
 CO
CO  28
28  1
1
28  CO
CO  CO = 40
CO = 40
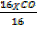 = 40
= 40 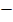 44
44
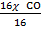 =
= 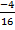
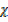 CO = 0.25
CO = 0.25
% Of CO = 25%
% Of CO2 = 75%