VAN DER WAAL EQUATION
The deviation of real gases from ideal behaviour has been stuglied by different scientist such as Amagat who deter minal different curves in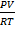 
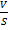P
Later on van der wall explained the deviation and gave his equation which tries to work / take particle volume and attraction into account
In his equation
i) He subtracted the particle volume from the volume of the container. If the volume of container is V and that of particular be presented as “b”
Then the total volume of the system will be
V 
b
This is called “Volume correction”
ii) He also added change in pressure which is caused by the existence of intermolecular forces of attraction among the gaseous molecules
This
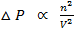
But n = 1 for 1mole
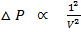
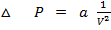
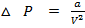This is correction in pressure.
From ideal gas equation
PV = nRT (n = 1)
PV = RT
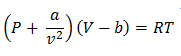
For one mole of the gas
Where “a” is a van der Waal constant
Note
In the van der Waal equation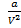 
is added to the total pressure in order to cancel the effect of intermolecular forces of attraction
Expansion of the Van der waal equation
From Van der Waal’s equation
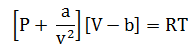
PV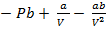 
PV = RT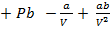 
The equation normally work under two assumption these is
If pressure is small then the volume is maximum
The terms Pb and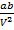 
can be neglected
PV = RT – a/V
ii) When the pressure is very low that is P is approaching O P O
So V will be infinity V is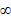 
We can calculate that the three term for correction can be neglected
PV = RT
This is for one mole
General conclusion
At very low pressure the real gases normally behave as ideal gases