Form 5 Chemistry – PHYSICAL CHEMISTRY – Three Components Liquid System

4. OSMOTIC PRESSURE

What is osmotic pressure ?

Osmotic pressure: Is the force per unit area which occur as the results of solvent to flow From low concentration to the high concentration of solute through a semi permeable membrane .

Osmotic pressure causes the osmosis to take place.

Osmosis: Is the tendency of solvent molecular to migrate from the region of low concentration to the region of high concentration of solute.

Consider the simple experiment below

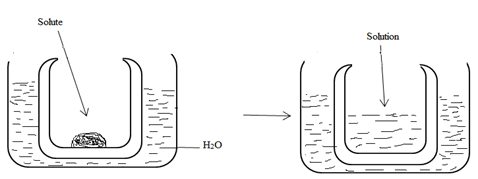
Factors affecting the Osmotic pressure of the substance

The Osmotic pressure of the substance affected by the two factors

    i) Concentration or volume of the solvent.

    ii) Temperature

i) CONCENTRATION OR VOLUME OF THE SOLVENT

The osmotic pressure of the substance varies directly proportional to the concentration and inversely proportional to the volume .

i.e An increase in concentration of the solution will cause an increase in osmotic pressure of the solution.

Also increases in osmotic pressure cause the decrease in volume.

ii) TEMPERATURE

The temperature varies directly proportional to the osmotic pressure as long as the temperature do not exceed the optimum temperature of the semi permeable membrane.

The effect of two factors above are explained by Vant- hoff’s laws of osmotic pressure.

VANT – HOFF’S LAWS OF OSMOTIC PRESSURE

Vant – hoff tried to put forward his laws which explain the variation of osmotic pressure with concentration and temperature.

There are two laws developed, These are:

    i) Vant- hoff”s first law of osmotic pressure.

   ii) Vant – hoff’s second laws of osmotic pressure.

i) VANT – HOFF’S FIRST LAW OF OSMOTIC PRESSURE

It states that;

“The osmotic pressure of the solution is inversely proportional to its volume”

Let the osmotic pressure be denoted by π

From 1^st law

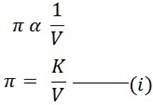
ii) VANT – HOFF’S SECOND LAW OF OSMOTIC PRESSURE

It states that;

“The osmotic pressure of the solution is directly proportional to temperature”

From 2^nd law

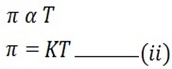
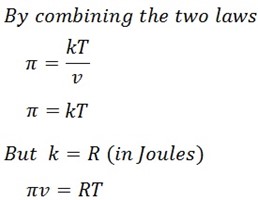
This is for 1 mole, But for ‘n’ mole the formula will be

   

Example1

7.85g of the compound Y having the empirical formula of C₅H₄ was dissolved in 301g of Benzoic (C₆H₆) . If the freezing point of the solution is 1.05^oC below that of pure benzene.

    i) Determine the molecular mass of  Y

   ii) Find the molecular formula of  Y if kf for C₆H₆ is 5.12^oC kg mol^-1

Solution

Mass of solute = 7.85g

Mass of solvent = 301g

F . P depression ΔT = 1.05^oC

Kf of solvent = 5.12^oC kgmol^-1

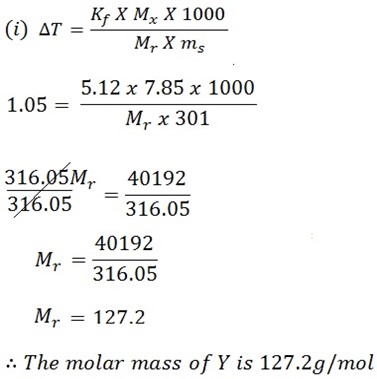
Example 2

Calculate the molar mass of solute given that 35g of solute dissolved in 1dm³ has osmotic pressure of 5.51 N/M² at 20^oC. (R = 8.314 Jmol^-1k^-1)

Solution

Mass of solute = 35g

Volume of solution = 1dm³

Osmotic pressure π = 5.51

Temperature T = 20^oC + 273k

= 293k

πv = nRT

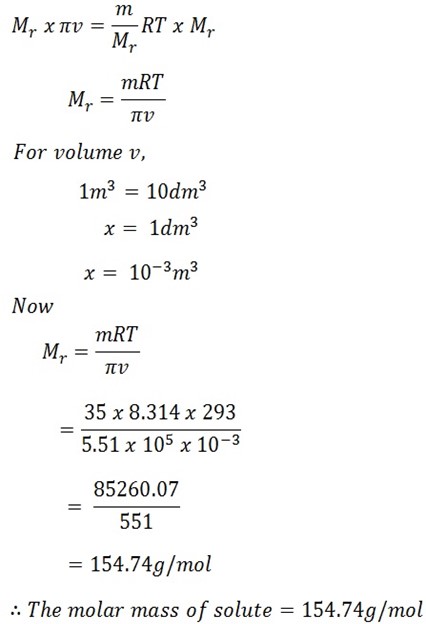
Example 3

a) Define

    i) Osmosis

   ii) Osmotic pressure

b) Differentiate between osmosis and diffusion

Answers
a) i. Osmosis : Is the tendency of a solvent molecules to move from the region of law concentration to the region of high concentration of solute.

   ii. Osmotic pressure : Is the force per unit area which occur as the result of solvent to flow from low concentration to the high concentration of solute through a membrane.

b) Osmosis is the movement of solvent molecules from the region of low concentration to the region of high concentration of solute through a semi- permeable membrane while Diffusion is the movement of gases molecules from the region of high concentration to a region of low concentration .

c) Calculate the osmotic pressure of the following solution at 25^oC

    i) Sucrose solution of concentration 0.213M (527.72 N/m²)

   ii) A solution of glucose (C₆H₁₂O₆) made by dissolving 144g/dm³ . (1.1982 x 10⁶ N/m²)

c) Solution

Temperature T = 25^oC + 273

                        = 298k

Molarity = 0.213M

(ii) Molar mass of glucose = 180

Concentration = 144g/dm³ = 144000g/m³

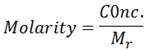
              = 144000 ÷ 180

              = 800M

Osmotic pressure π = MRT

                 = 800 x 8.314 X 298

                 = 1.982 X 10⁶N/M²

  ∴ The osmotic pressure of a solution = 1.982 X 10⁶ N/M²

Example 4

Calculate the osmotic pressure of the solution containing 12g of C₆H₁₂O₆ in 300g of water at 20^oC.

R = 8. 314 Jmol ^-1k^-1(54.13 X 102 N/m^-2).

Solution

Mass of solute = 12g

Mass of water = 300g  hence volume = 300cm³

Temperature T = 20^o + 273
= 293k

But
1m = 100cm

    1m³ = 100³cm³

     X = 300cm³
              100³

     X = 3 X 10 ^-4

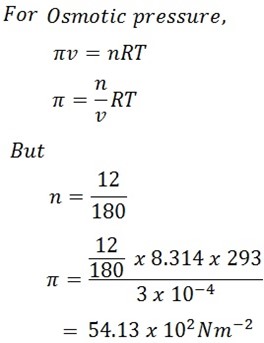
Example 5

Calculate the osmotic pressure of 10% glucose solution at 50^oC  R= 8.314 Jmol^-1k ^-1

Solution

Temperature T = 50^oC + 273

                      = 323k

Mass = 10% glucose

Molar mass of glucose = C₆H₂O₆

                                 = 180

 Example 6

37.44g of haemoglobin, the protein of red blood cell which carries the oxygen in the blood, were dissolved in a dm³ of water.

The solution formed had an osmotic pressure of 1.37 kPa  at body temperature of 37^oC.

Determine the molar mass of haemoglobin.

Solution

Mass of solute = 37.44g

Volume = 1 dm³

Temperature = 37^oC + 273k

                                           =310k

Osmotic pressure = 1.37 kPa X 1000

                             = 1370Pa

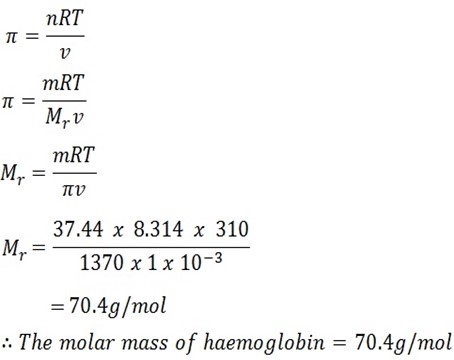
Example 7

A solution containing 10g of solute A in 300. Of water has an osmotic pressure of 375mm of 25^oC. What will be the osmotic pressure be dissolving 2.55g of solute A in 50g of water? R = 0.0821 atm mol^-1 k ^-1 L.

Solution

Mass of solute A M_A =10g

Volume of solvent = 300cm³ = 0.3m³

Osmotic pressure = 375mmHg

                 1 atm = 760mmHg

                 X = 375mmHg

                 X =  375
                         760

                     = 0.49

Temperature T = 25^oC + 273k

                      = 298k

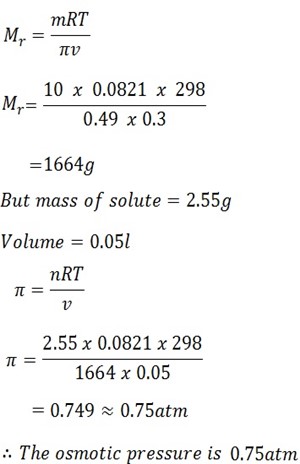
 COLLIGATIVE PROPERTIES OF ASSOCIATIVE AND DISSOCIATIVE SOLUTE

Colligative properties depends on vant hoff’s factor . Vant  hoff  factor is the ratio of observed colligative properties to that of calculated colligative property.

OR

Vant hoff factor is the ratio of experimental colligative property to that of theoretical colligative property.

VANT HOFF FACTOR

Vant hoff’s factor is denoted by ‘g’ or ‘l’ and therefore

Vant’s hoff  factor is obtained when the solute added is not completely ionized (dissociated).
Also some solutes, when added in the solvent tend to associate.

The phenomena of associating or dissociating of solute is explained in terms of degree (degree of association or dissociation).

The degree of dissociation is

Define:

The degree of dissociation is the percentage or fraction of moles of ions which have gone into the solution.

     It is denoted by α

The degree of dissociation is related to Vant hoff’s factor and the number of ions formed by the solute dissolved.

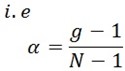
Where by;

      α is the degree of dissociation

      g is the Vant hoff’s factor

      N is the number of ions

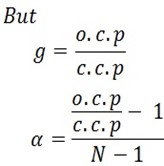
Example 1.

Calculate the N values  for the ionization of the following compounds

Solution

i) Al ( OH)₃

Ionization equation

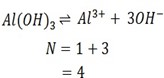
ii) FeCl₃

Ionization equation

iii) BaCl₂

Ionization equation

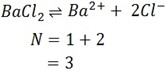
iv) NaCl

Ionization equation

             

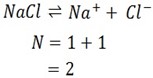
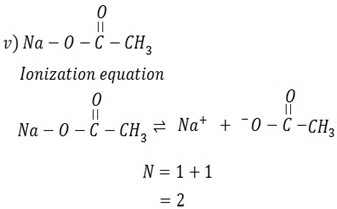
NOTE

The degree of dissociation can be expressed terms of

      i) Percentage%

     ii) Decimals

When it is expressed in percentage it cannot exceed 100% and

When it is expressed in decimal it cannot exceed 1.00

     Also when solute is ionizing completely its degree of dissociation become 100%  OR  1.00

Example 2.

What will be the boiling point of the solution containing 2.4g NaCl in 250cm³ of water . it an aqueous solution of NaCl is 70% Dissociation.

(kb water = 1.86)

Solution

Mass of solute m_x = 2.4g.

Mass of solvent m_s = 250g.

Kb = 1. 86.

α = Degree of elevation 70% or o.7http://192.168.137.101/tz/cexam.php?MASTexam=586

M_rx = NaCl

        = 23 + 35.5

        = 58.5 g/mol

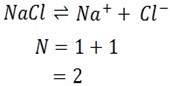
Δ T = Kb x m x 1000
              m_s X Mr_x

       = 1.86 x 2.4 x 1000
               250 x 58.5

      = 0.305^oC

c.c.p = 0.305^oC