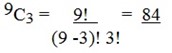SUBTOPICS
i) Permutation and combination
ii) Probability of an event
iii) Combined events
iv) Mutual exclusive events
v) Independent events
vi) Application of probability
1. PERMUTATIONS AND COMBINATIONS
Deal with arrangements of objects
Factorial notation
Consider the following pattern
2 x 1 = 2
3 x 2 x 1 = 6
4 x 3 x 2 x 1 = 24
5 x 4 x 3 x 2 x 1 = 120
6 x 5 x 4 x 3 x 2 x 1 = 720
Generally
If you have and different objects, you can get
n x (n – 1) x (n – 2) x (n – 3) x….. 3 x 2 x 1 different arrangements
n x (n – 1) x (n – 2) x (n – 3) x…… x 3 x 2 x 1 is called n – factorial denoted by n!
Examples
2! = 2 x 1= 2
3! = 3 x 2 x 1 = 6
4! = 4 x 3 x 2 x 1 = 24
5! = 5 x 4 x 3 x 2 x 1 = 120
6! = 6 x 4 x 3 x 2 x 1 = 720
0! = 1
Exercise
1. Evaluate each of the following
a) 6!
b) 8! / 3!
c) (7 – 2)!
d) 3! / 0!
e) 5! / (5 – 2)! 2!
2. Simplify
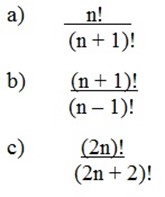
3. Write the following in factorial form
a) 4 x 3 x 2 x 1
b) 6 x 5 x 4
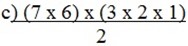
Solution
1. a. 6! = 6 x 4 x 3 x 2 x 1 = 720
b. 8! / 3! = 
= 
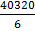= 6720
c. (7 – 2) !
5! = 5 x 4 x 3 x 2 x 1 = 120
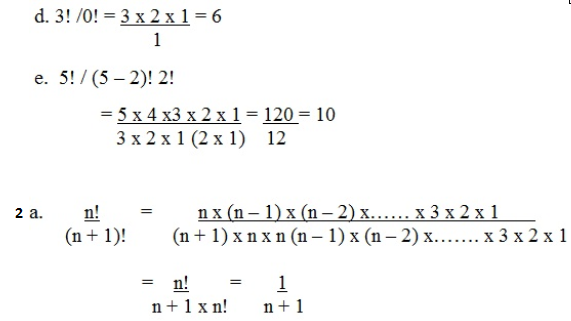
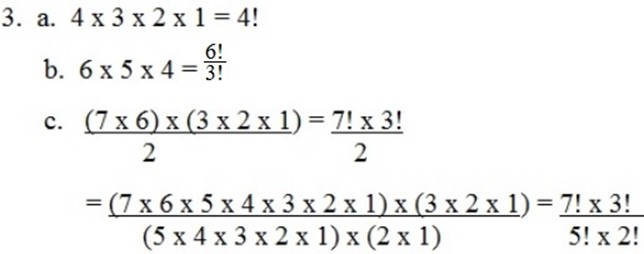
PERMUTATION AND COMBINATIONS
WAYS OF ARRANGING UNLIKE OBJECTS
Examples
1. How many different three numbers can be formed using the digits 9, 6 and 3
Solution
Digits 9, 6, 3
Ways of science 3 3 3
The total number of ways is 3 x 3 x 3 = 27
2. How many 3 letters groups can be formed using the letters 0, N and W provide each letter is used once?
Solution
Letters O N W
Ways of selective 3 2 1
Total number of ways = 3 x 2 x 1
= 6
PERMUTATIONS
Is arrangement of objects in a particular order.
Example
1. How many ways three letters A B C can be arranged taking three at a time?
Solution
ABC, BCA, BAC, CAB, CBA, ACB
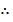There are 6 ways ie 3p3 = 6
Note:
i) The upper 3 indicates the total number of objects
ii) The lower 3 indicates the number of items used in making arrangements
ii How many three letters A, B, C can be arranged taking two at a time?
Solution.
AB, BA, CA, AC, BC, CB
There are 6 ways
i.e. 3p2 = 6
Note
The order of arrangement matters
i.e. AB is different permutation from BA
Generally
To find npr i.e. the number of permutation of n different objects taking r at a time can be arranged as follows.
– The 1st place can be filled in n different ways
– The 2nd place can be filled in (n – 1) different ways
– ” 3rd place ” ” ” ” (n – 2) ” ”
– rth ” ” ‘ ‘ (n – r + 1) ” ”
nPr = n (n – 1) (n – 1) …… (n – r + 1) ……..i
eqn (i) can be multiplied and divided by (n – r) (n – r – 1) …….x 3 x 2 x 1
eqn i) becomes
2) How many arrangements can be made from the word mathematics?
solution
m = 2, a = 2, t = 2
n =11
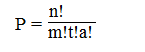
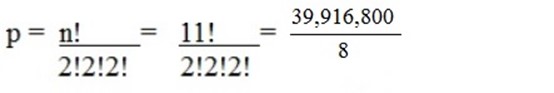
= 4, 989,600
COMBINATIONS
– Is the selection of objects where order is not important
Example (1)
Three letters ABC may be arranged taking three at a time as follows
ABC, BCA, BAC, CAB, CBA, ACB
– These are different permutations but the same combination
– Denoted by, 3C3 = 1
Examples (2)
We may take the same letters; find the numbers of selections of the letters ABC, taking two at a time
AB, AC, BC, BA, CA, CB
AB, AC, BC
3C2
Examples (3)
In how many ways can r objects be chosen from n unlike objects?
The number of combination of n objects taking at time can be arranged in r!
The number of combination of n objects taking r at a time can be arranged in r
The numbers of permutations
= r! x nCr
Note:
i) nCr may be written as
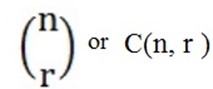
ii) nCo = 1, nCn = 1, nC1 = n
Examples (4)
A mixed hockey team containing 5 men and 6 women is to be chosen from 7 men and 9 women in how many ways can this be done?
Solution
5 men can be selected from 7 men in, 7C5 ways
6 women can be selected from 9 men in, 9C5 ways
The combination will be,
7C5 x 9C6
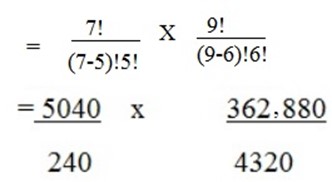
= 21 x 84
= 1,764 ways
Examples (5)
Tabulate the different selections of two letters that can be made from the letters TAKEN, deduce the value of 5C2
Solution
TAKEN
TA, TK, TE, TN, AK, AE, AN, KE, KN, EN
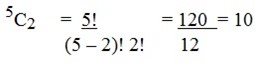
Examples 6
In how many ways can a cricket team be selected from 13 players? Hint a cricket team has 2 players.
Solution
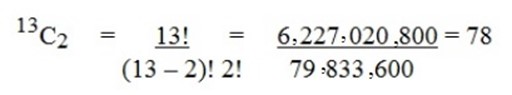
Examples 7
In ow many ways can a football team of 11 players can be chosen from a class of 15? In how many ways can be the 4 spectators be chosen
from the class of 15?
Solution
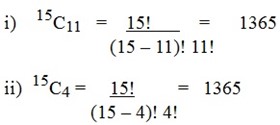
Note:
nCr = nCn-r
Exercise
1. From a list of 30 books, how many different groups of 22 books can be selected?
Solution
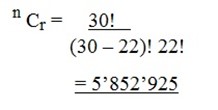
2. How many different netball teams of 7 members can be formed from 18 players?
Solution
nCr = 18C7
= 18!
(18 – 7)! 7!
= 31′ 824
3. A circle has 10 marked points, how many different & three – sided figures which can be formed by joining any three of these points
Solution
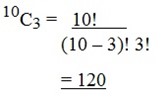
4. How many different committees comprising of 20 people can be formed from 25 people?
Solution
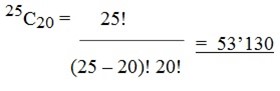
5. If a plane paper has 9 points in which no three points appear on the same straight line, how many distinct triangles can be formed by joining any three points?
Solution
