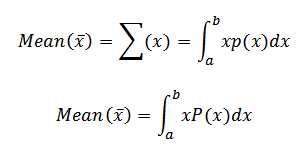THE EXPECTATION AND VARIANCE OF ANY FUNCTION
i) E (a) = a
Where a = is a constant
Proof
E (x) = 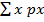
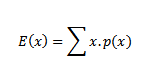
But
P (x) = 1
E (a) = a (s)
E (a) = a proved
ii) E (ax) = a E (x)
Where
a = constant
Proof
E (x) = 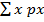
E (ax) = 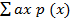
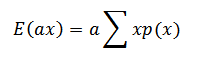
But
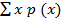 = E (x)
= E (x)
E (ax) = a E (x) proved
Where a and b are constant
Proof – 03
E (x) = Ex p (x)
E (ax + b) = 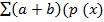
= 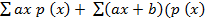
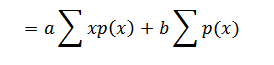
= a E (x) + b (1)
E (ax + b) = a E (x) + b. Proved
4. Var (x) = 0
Where a – is constant
Proof 4
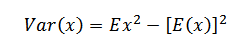
a2 – (a) 2
= a2 – a2
= 0 proved
5. var (ax) = a2 var (x)
Where
a – is any constant
Proof 05
Var (x) = E (x2) – [E (ax)] 2
var (ax) = E (ax) 2 – [E (ax) ] 2
= E (a2 x2) – [aE (x)] 2
= a2 E (x2) – a2 (E (x)] 2
= a2 E (x2) – a2 [E (x)] 2
= a2 [E (x2) – a2 [E (x)] 2
= a2 [E (x2) – [E (x)] 2]
var (x) = a2 var (x)
Var (ax + b) = a2var (x)
Where a and b are constant
Proof
Var (v) – E (ax + b) 2 – [E (ax + b)] 2
Var (ax + b) = E (ax + b) 2 – [E (ax + b)] 2
Var (ax + b) – E (a2x2 + 2abx + b2) – [a Ex + b) 2
= E (a2x2) + E (2abx) + E (b2) – [a2 E2 (x) + 2ab E (x) + b2
a2 E (x2) + 2abE (x) + b2 – a2 E2 (x)
8. For random variable x show that var (x) – E (x2) – [E (x)] 2
b) The random variable has a probability density function p (x = x) for x = 1, 2, 3. As shown in the table below.
| X | 1 | 2 | 3 |
| P (x) | 0.1 | 0.6 | 0.3 |
edu.uptymez.com
Find i) E (5x + 3)
ii) E (x2)
iii) var (5x + 3)
Consider the nglish-swahili/distribution” target=”_blank”>distribution table
| X | 1 | 2 | 3 |
| P (x) | 0.1 | 0.6 | 0.3 |
| Xp (x) | 0.1 | 1.2 | 0.9 |
| X2 | 1 | 4 | 9 |
| x2 Px | 0.1 | 2.4 | 2.7 |
edu.uptymez.com
∑(5x + 3) = 5∑(x) + 3
But
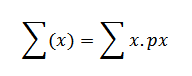
= 0.1 + 1.2 + 0.9
= 2.2
 = 5 (2.2) + 3
= 5 (2.2) + 3
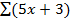 = 14
= 14
ii)
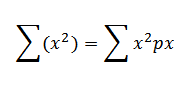
= 0.1 + 2.4 + 2.7
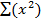 = 5.2
= 5.2
iii) Var (5x + 3) = 52 var x
= 25 var (x)
Var (x) = 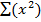 – [
– [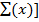 2
2
Var (x) = 5.2 – (2.2) 2
Var (x) = 0.36
Hence
Var (5x + 3) = 25 (0.36)
Var (5x + 3) = 9
Example
The discrete random variable x has probability nglish-swahili/distribution” target=”_blank”>distribution given in the table below;
Find var (2x + 3)
| X | 10 | 20 | 30 |
| P (x) | 01 | 0.6 | 0.3 |
edu.uptymez.com
From the given table
Var (2x + 3) = 22 var (x)
= 4 var x
But
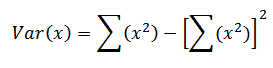
Distribution table
| X | 10 | 20 | 30 |
| P (x) | 0.1 | 0.6 | 0.3 |
| Xp (x) | 1 | 12 | 9 |
| X2 p (x) | 100 | 240 | 270 |
| X2 | 100 | 400 | 900 |
edu.uptymez.com

= 1 + 12 + 9
= 22

= 10 + 240 + 270
= 520
Var (x) = 520 – (22) 2
Var (x) = 36
Therefore
Var (2x + 3) = 4 var (x)
= 4 (36) = 144
Var (2n + 3 = 144
BINOMIAL DISTRIBUTION
This is the nglish-swahili/distribution” target=”_blank”>distribution which consists of two probability values which can be distributed binomially
Properties
It has two probabilities, one is probability of success and one is a probability of failure.
The sum of probability of success p and of failure of q is one
P + q = 1
The trial must be independent to each other
It consist of n – number of trials of the experiment
Hence;
If p is the probability that an event will happen i.e ( probability of success) and q is the probability that the event will not happen i.e (probability of failure) where n – is the number of trials
Then
The probability that an event occurs exactly x time from n – number of trials is given by
P(x) = ncx px qn –x
Where
n = is the number of trials
q = is the probability of failure
p = is the probability of success
x = is the variable
MEAN AND VOLUME , 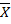
Recall
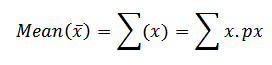
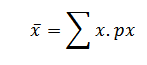
 =
=  cx p x q n – x
cx p x q n – x
Where
x = 0, 1, 2, 3…..n
 = 0nC0p0qn – 0 + 1nC1p q n- 1
= 0nC0p0qn – 0 + 1nC1p q n- 1
+ 2n C2 p2qn – 2 + 3n C3P3qn- 3
+……..n.nCn pn qn – n
= nC1pqn – 1 + 2n C2p2qn – 2 +
3n C3 p3 qn – 3 +……+nn Cn pnqo
= 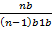 pq n – 1 +
pq n – 1 + 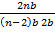 p2qn – 2
p2qn – 2
= 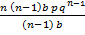 +
+ 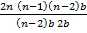
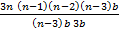 +…….+ npn
+…….+ npn
= npqn – 1 + n (n – 1) p2qn – 2 +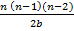 p3qn – 3 + …..npn
p3qn – 3 + …..npn
= np [qn – 1 + 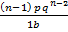 +
+ 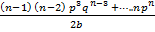
= np [qn – 1 + 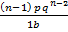 +
+ 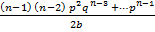
= np (p + q) n -1
But
P + q = 1
= np (1) n -1
= np

VARIANCE
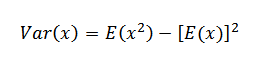
Taking
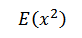
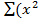 ) =
) = 
= 
 ) =
) = 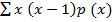
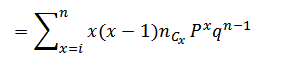
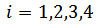
= On C1p1qn – 1 + 2nC2P2qn – 2 + 6nC3P2qn – 3….. + n (n – 1) nCnpnqn
= 2nC2p2qn-2 + 6n C3 p3q n – 3 + ….. + n (n – 1) nCn Pnq0
=  p2qn – 2 +
p2qn – 2 +  +…… + n
+…… + n 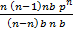
= 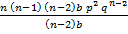 +
+ 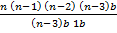 + …… + n (n – 1) pn
+ …… + n (n – 1) pn
= n (n – 1) p2qn – 2 + 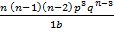 + n (n – 1) pn
+ n (n – 1) pn
= n (n – 1) p2 [qn – 2 + 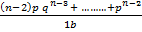 ]
]
= n (n – 1) p2 (p + q) n – 2
= p (n – 1) p2
Hence
∑(x2)= n (n – 1) p2 + np
= np (n – 1) p + 1)
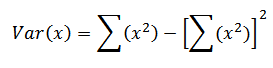
= np (n – 1) p + 1) – (np)2
= np [(n – 1) p + 1 – np]
= np [np – p + 1 – np]
= np [1 – p]
= npq
Var (x) = npq
STANDARD DEVIATION
From S.D = 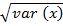
S.D = 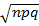
Note
From p (x) = nCx px qn – x
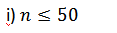
ii) 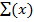 = np
= np
iii) var (x) = npq
iv) S.D = 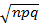
Question
1. A pair coin is tossed 12 times the probability of obtaining head is 0.5, determine mean and standard deviation.
2. If x is a random variable such than 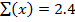 and p = 0.3
and p = 0.3
Find the value of n and S.D
3. Suppose that, the rain office records. Show that averages of 5 days in 30 days in June are rainy days. Find the probability that June will have exactly 3 rainy days by using binomial nglish-swahili/distribution” target=”_blank”>distribution also find S.D.
POISSON DISTRIBUTION
This is the special case of binomial probability nglish-swahili/distribution” target=”_blank”>distribution when the value of n is very large number (n > 50) and when the probability of success, p is very small i.e (p < 0.1)
Properties
The Condition for application of poison probabilities nglish-swahili/distribution” target=”_blank”>distribution are
i) The variable x must be discrete random
ii) The occurrence must be independent
iii) The value of n is always greater than 50 (i.e n) 50) and the probability of success, p is very small i.e p<0.1
iv)

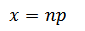
Therefore;
P (x) = nCx pxqn – x
But p + q = 1
q = 1 – p
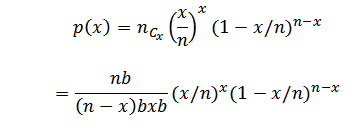
= 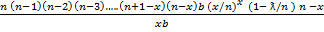
= 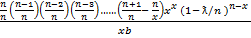
= 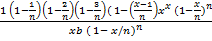
= 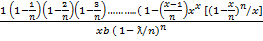
But
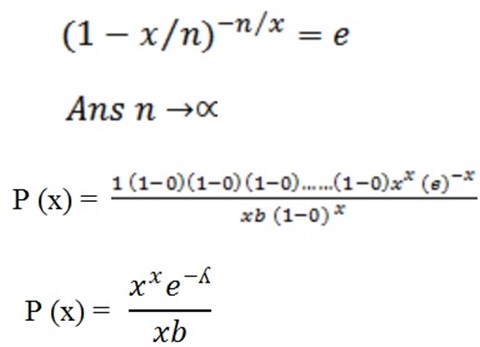
Note;
(1 + 1/x) x = e
X = ∞
MEAN AND VARIANCE
From 
= 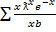
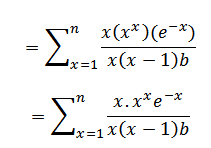
Where
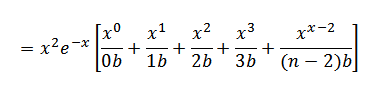
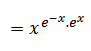
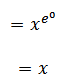
Therefore
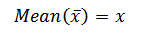
= np
Variance
Var (x) = 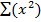 – E2 (x)
– E2 (x)
Taking
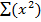 = n
= n 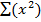
But
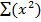 =
= 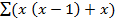
= 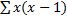 +
+ 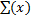
Taking

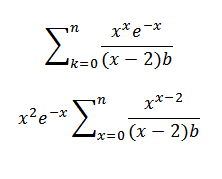
Where;
i = 2, 3, 4
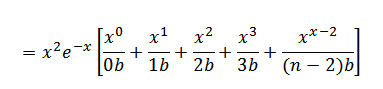
= x2 e –x. ex
= x2
Hence,
∑ x (x – 1)
∑ (x2) = ∑x (x – 1) + ∑(x)
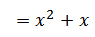
Therefore;
Var (x) = ∑(x2) – ∑2 (x)
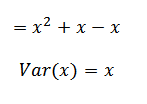
Var (x) = np
STANDARD DEVIATION
From
S.D = 
= 
S.D = 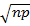
Question
1. Given that probability that an individual is suffering from moralia is 0.001. Determine the probability that out of 2000 individual
i) Exactly 3 will suffer
ii) At least 2 will suffer
2. Use poison nglish-swahili/distribution” target=”_blank”>distribution, find the probability that a random sample of 8000 people contain at most 3 NCCR members if an average 1 person in each 1000 members is NCCR member.
3. Random variable x for a poison nglish-swahili/distribution” target=”_blank”>distribution, if
P (x = 1) = 0.01487
P (x = 2) = 0.0446. Find
P (x = 3)
b) Find the probability that at most 5 defective fuses will be found in a box of 200 fuses of an experience shows that 2% of such fuses are defective.
B. CONTINUOUS PROBABILITY DISTRIBUTION
These are two parts of continuous probability nglish-swahili/distribution” target=”_blank”>distribution, these are
i) The variable x must be continuous
ii) The function is integrable
iii) The area under the curve are
= 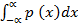
iv) For the curve f (x)
i.e f (x) > 0 or f (x) ≥1
RULES
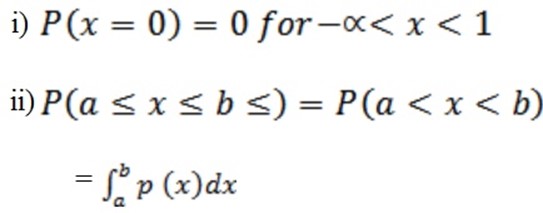
iii) P (x < x) = 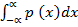
For instance
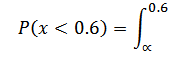
iv) P (x > x) = 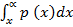
For instance
P (x > 0.2) = 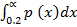
· Note
The sufficient conditions for p (x) to be continuous nglish-swahili/distribution” target=”_blank”>distribution are
i) P (x > o) at (a, b)
ii) Area under the curve is 1 i.e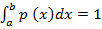
Mean variance by probability density function (p.d.f)