NORMAL CURVE
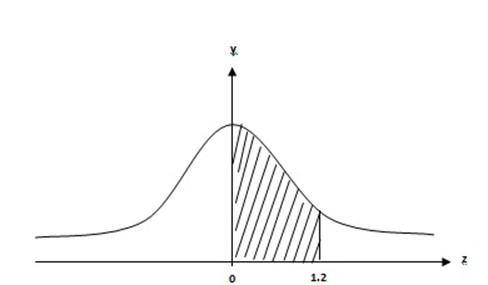
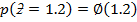
Area = 0.3849sq unit
(d) 
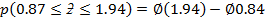
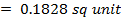
(e)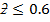 
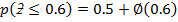
= 0.7258
(f)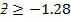 
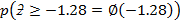
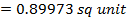
Question
Determine the normalized variety (→t)p(t) for x=53 and normal nglish-swahili/distribution” target=”_blank”>distributions
P(t) for the following data 55, 54, 51,55, 53, 53, 54, 52
Solution
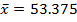
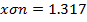
From
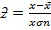
By using scientific calculation
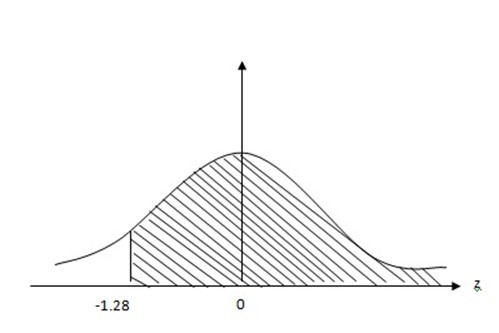
53 – t
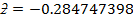
= -0.28
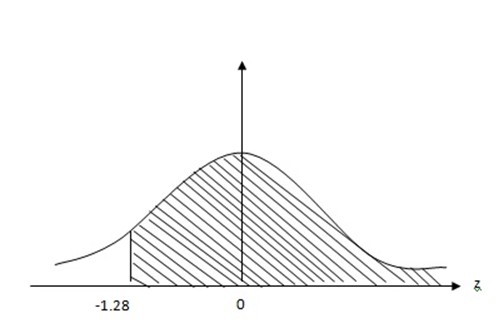
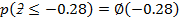
= 0.38974
Question
The marks in Mathematics examination are found to have approximately normal nglish-swahili/distribution” target=”_blank”>distribution with mean 56 and standard deviation of 18. Find the standard mark equivalent of a mark 70.
Solution
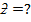
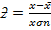
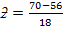
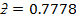
= 0.78
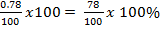
= 78%
The standard mark equivalent to a mark of 70 is 78%
Question
Assuming marks are normally distributed with means 100 and standard deviation 15. Calculate the proportional of people with marks between 80 and 118
Solution
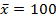
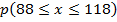
But
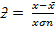
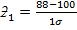
= -0.8
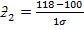
= 1.2
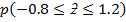
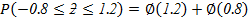
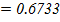
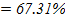
The proportional of the people with marks between 88 and 118 is 67.31%
Question
(a State the properties of normal nglish-swahili/distribution” target=”_blank”>distribution curve
(b Neema and Rehema received standard score of 0.8 and 0.4 respectively in Mathematics examination of their marks where 88 and 64 respectively. Find mean and standard deviation of examination marks.
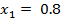
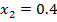
From
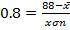
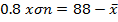
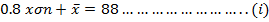
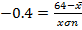
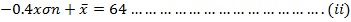
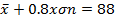
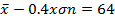
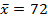
THE NORMAL APPROXIMATION (N) TO THE BINOMIAL DISTRIBUTION (B)
Suppose x is the discrete variety distributed as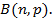 
then this can be approximately 
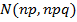if and only if
(i)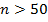 
(ii) P is not too large or too small re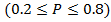
Note:
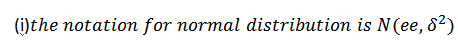
(ii)
(A normal approximation to binomial nglish-swahili/distribution” target=”_blank”>distribution)
For x considered as 
Then
– For x considered as approximate by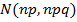 
Then
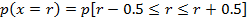
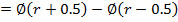
Questions
24: A fair win is tested 400 times; find the probability of obtaining between 190 and 210 heads inclusive.
Solution
Given
N= 400
P = ½
B = (400, ½ )
Also
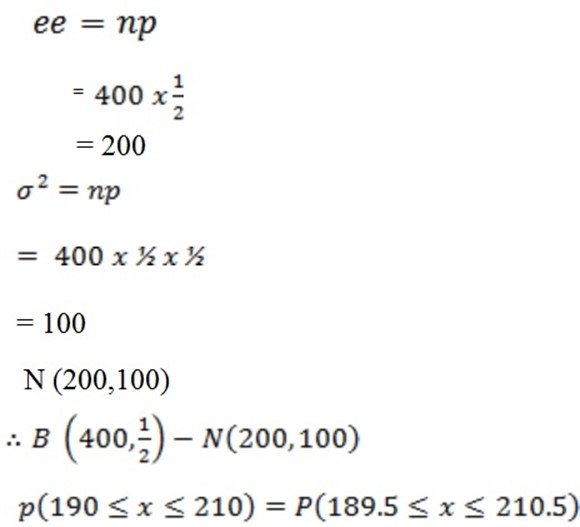
From
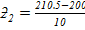
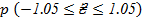
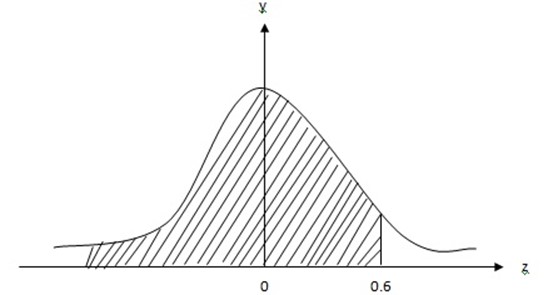
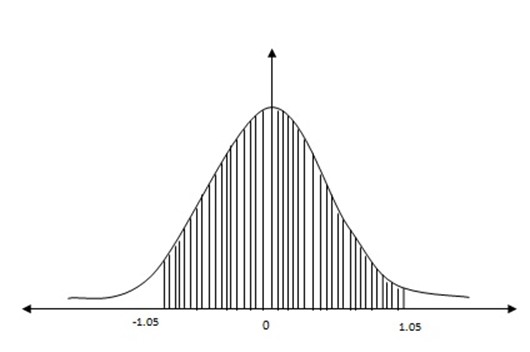
Normal curve
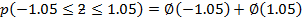
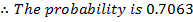
25. Find the probability of obtaining between 4 and 6 head inclusive in 10 tosses of fair coin.
(a) Using the binomial nglish-swahili/distribution” target=”_blank”>distribution
(b) Using the normal nglish-swahili/distribution” target=”_blank”>distribution
Solution
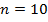
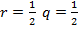
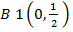
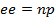
= 5
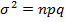
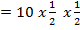
= 2.5
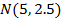
(a) Using the binomial nglish-swahili/distribution” target=”_blank”>distribution
=
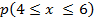
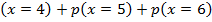
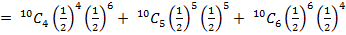
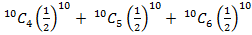
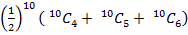
= 0.6563
The probability is 0.6563
(b) By using normal nglish-swahili/distribution” target=”_blank”>distribution
re
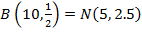
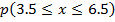
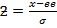
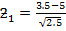
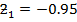
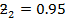
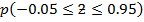
Normal curve
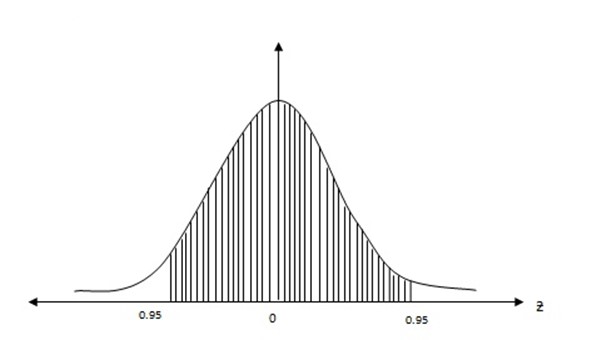
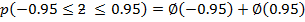
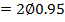
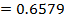
The probability is 
(26) Find the probability of obtaining form 40 to 60 heads in 100 tosses of a fair coin
(27) (a) A binomial experiment consists of “n” trials with a probability of success “p” an each trial.
(i) Under what condition be used to approximate this binomial nglish-swahili/distribution” target=”_blank”>distribution.
(ii) Using the conditions named in (i) above, write down mean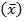 
and standard deviation
(b) The probability of obtaining head is ½ when a fair coin is tossed 12 times.
(i) Find the mean 
and standard deviation for this experiment
(ii) Hence or otherwise, approximate using normal nglish-swahili/distribution” target=”_blank”>distribution the probability of getting heads exactly 7 times
(a) (i) The condition are
Solution
The condition are
n>50
p is not too large or too small
(0.2 ≤ p≤ 0.8)
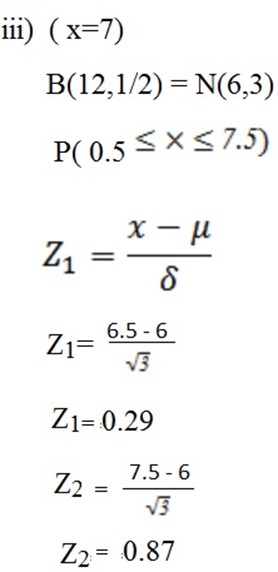
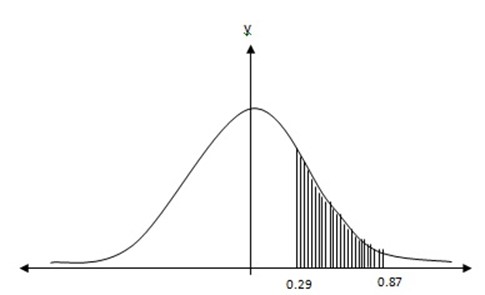
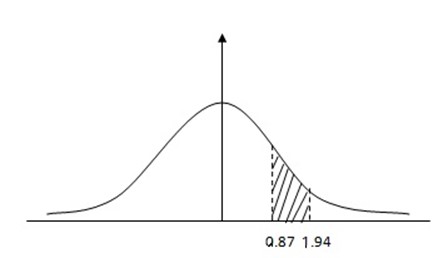
P(0.29 ≤ Z ≤ 0.87) =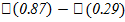
The probability of getting head exactly of 7 times is 0.1938.
28) A machine producing rulers of normal length 30cm is examined carefully and found to produce rulers whose actual lengths are distributed as N(30,0.0001) Find the probability that a ruler chosen at random has a length between 30cm and 30.01 cm
Soln # 28
N (30,0.0001)
µ=30, 
P (30 ≤ × ≤ 30.01)
Z =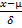
Z1= 30-30
0.01
Z1 = 0
Z2 = 30.01-30
=0.01
Z2 = 1
P(0 ≤ z ≤ 1 )
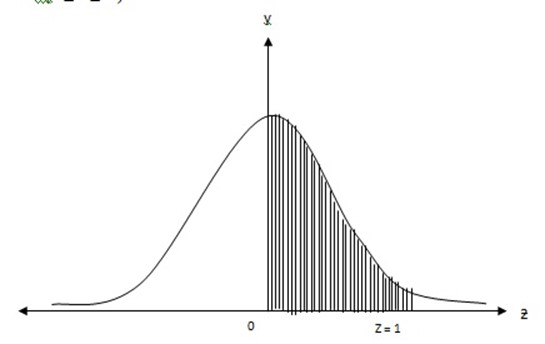
P (0 ≤ z ≤ 1) = ɸ (1)
= 0.3413
Probability is 0.3413