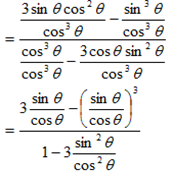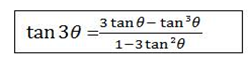APPLICATIONS OF PYTHAGORAS IDENTITY
I. SOLVING TRIG EQUATIONS
Example 1.
Solve the equation 1 + 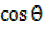 –
– 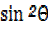 = 0 for the values of the values (θ) between 00 and 3600 inclusive.
= 0 for the values of the values (θ) between 00 and 3600 inclusive.
Solution:
1 + 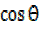 –
– 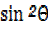 =0
=0
But from Pythagoras identity
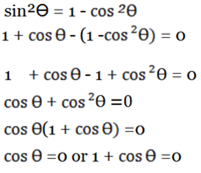
cosθ = 0,cos θ =-1
case of cosθ = 0
θ=cos–(0)
θ=900
θ=900,2700
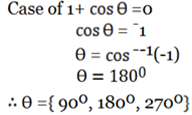
Example 2.
Solve for the values of x between 00 and 3600 inclusive of
(i) Tan 4x + 7 = 4sec2x
(ii) -6sm2x – cosx + 5 =0
Solution
Tan4x + 7 =4sec2x
But tan2x + 1 =sec2x
Tan4x + 7=4(tan2x + 1)
Tan4x + 7 =4tan2x + 4
Tan4x +7-4tan2x -4 =0
Tan4x -4tan2x + 3 =0
Let tan2x =m
Then m2 – 4m +3 =0
m2 -3m –m + 3 =0
m(m -3)-1(m-3)=0
(m – 1)(m-3) =0
m – 1 =0, m- 3=0
m= 1, m=3
Case 1 m =1 =tan2x
Tan x = 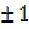
Tan x = 1
X = tan-1(1) = 450
X = 1800 + 450 = 2250
Tan x =-1
X= tan -1(-1)
X =180 450 =1350
X = 3600 -450=3150
Case 2: m3
Tan2x = 3, tanx=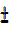
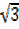
Tan x =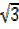
X = tan-1(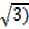 =600
=600
X =1800 + 600 =2400
tan x =-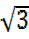
x = tan -1(-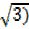
= 1800 -600=1200
X=3600 -600=3000
 x=
x=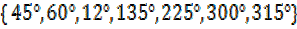 work on (ii)
work on (ii)
II PROVING IDENTITIES
Examples: prove the following identify
i) Tan2θ + sin2θ =(secθ + cosθ) (secθ – cosθ)
ii) Cot4θ + cot2θ =cosec4θ – cosec2θ
iii) 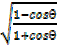 = cosecθ – cotθ
= cosecθ – cotθ
iv) 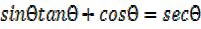
v) cosecθ –sinθ = cotθ
Solution: (i)
tan2θ + sin2θ = (secθ+ cosθ) (secθ –cosθ)
Delaying with R.H.s
Proof = (secθ + cosθ)(secθ – cosθ)
Then
=sec2θ – cos2θ
But sec2θ = 1+ tan2θ and
Cos2θ = 1 –sin2θ
=1 + tan2θ -(1 – sin2θ)
=1 + tan2θ -1 + sin2θ
=tan2θ+ sin2θ
 tan2θ+ sin2θ L.H.S proved
tan2θ+ sin2θ L.H.S proved
ii) cot4θ+ cot²θ= cosec4θ – cosec2θ
solution.
Dealing with L.H.S
Proof
=Cot4θ + cot2θ
then
=Cot2θ(cot2θ + 1)
But Cot2θ+ 1 =cosec2θ
Cot2θ =cosec2θ -1
(cosec2θ -1) cosec2θ
Cosec4θ – cosec2θ R.H.S
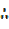 Cot4θ + cot2θ= cosec4θ – cosec2θ
Cot4θ + cot2θ= cosec4θ – cosec2θ

iv) sin θtanθ + cosθ=secθ
solution.
Proof
Dealing with L.H.S
Sinθtanθ+ cosθ
But tanθ = 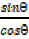
Then
Sinθ 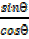 + cosθ
+ cosθ
 =
= 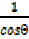 = secθ
= secθ
sin²θ + cos²θ =1 (Pythagoras identity)
 sin
sin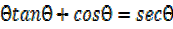

III) ELIMINATION PROBLEMS
Examples:
Eliminate ÆŸ from the following equations
i) Cosθ + 1 =x and sinθ =y
ii) X= a sinθ and y= btan θ
iii) X= 1 + tanθ and y = cos θ
iv) X= sinθ – cosθ
Y= cotθm+ tanθ
Solution.
(i) Cosθ + 1 =x
Cosθ=x – 1 ……… (i)
sinθ = y…………..(ii)
squaring equations (i) and (ii) the sum
cos²θ+ sin²θ= (x -1)² + y²
but sin²θ + cos²θ =1
then 1= (x – 1)² + y²
1 = x² – 2x + 1 + y²
x² + y2 -2x + 1 – 1 =0
x² +y²- 2x =0
ii) from x = a sinθ, sinθ=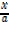
and from y=btanθ, tanθ=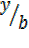
refer 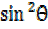 +
+ 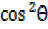 =1
=1
dividing by 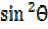 both sides
both sides
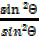 +
+ 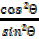 =
= 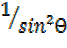
1+ 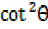 =
=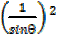
But 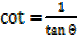
Then 1 +  =
= 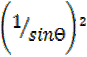
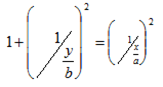
1 +  =
= 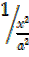
1 + 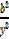 =
= 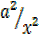
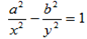
iii) X = 1 + 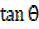
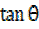 = x – 1 ……….. (i)
= x – 1 ……….. (i)
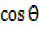 = y
= y
Refer, 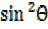 +
+ 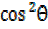 = 1
= 1
Dividing by 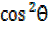 both sides
both sides
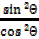 +
+ 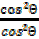 =
= 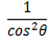
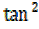 ÆŸ + 1 =
ÆŸ + 1 = 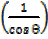
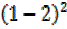 + 1=
+ 1= 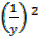
 + 1 =
+ 1 = 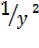
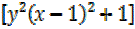 = 1
= 1
Solution (iv)
x =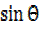 –
–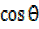 ………….(a)
………….(a)
Y = +
+ 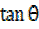 ……….(b)
……….(b)
From (b) 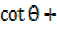
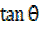
= 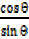 +
+ 
Y=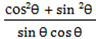 =
=
Y =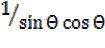
Squaring
x² = 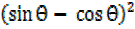
x² = 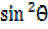 -2
-2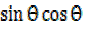 +
+ 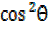
=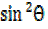 +
+ 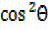 -2
-2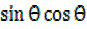
x² = 1- 2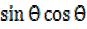
then
x² = 1 – 2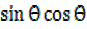
but 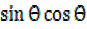 =
=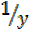
x² = 1 – 2
x² =1 – 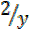
x² + 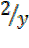 -1 =0
-1 =0
NB: In elimination problems concept is to eliminate the trig function in the equation, then try the possibilities of eliminating it by connecting it to the pythageras theorem (identity)
COMPLEMENTARY ANGLES
Consider the triangle below

 =
= 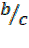 (i)
(i) 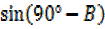 =
=  (iv)
(iv)
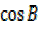 =
=  (ii)
(ii) 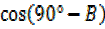 =
= (v)
(v)
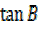 =
=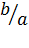 (iii)
(iii)  =
=  .(vi)
.(vi)
Thus

Is the condition for complementary angles
Definition: Complementary angles are angles whose sum is 90°
E.g: A + B = 90°
30° + 60° = 90°
30° and 60° are complementary angles.
NB: Supplementary angles are angles whose sum is 180°
Eg: A + B = 180°
Then A and B are supplementary angles
COMPOUND ANGLES FORMULA
Consider two angles say A and B then the angles A + B are called compound angles.
The concept here is to obtain
Sin (A ±B), Cos (A ±B), Tan (A ± B)
However it is easier to say that
Sin(A + B) = sin A + sin B
Testing if it is true
Let A= 60 and B= 30°
Sin(A + B) = sin(60° + 30°) = sin 90° = 1
Sin A + sin B = sin 60°+ sin 30°
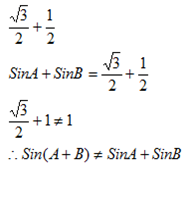
Consider the figure below
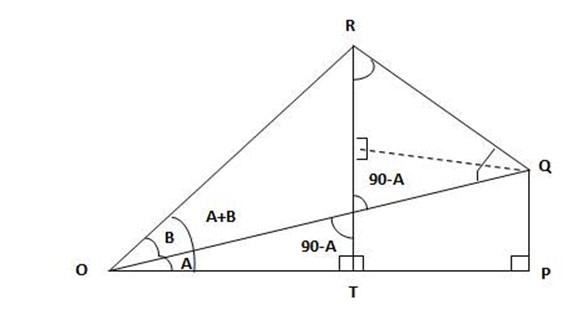
From  OTR
OTR
 =
= 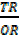
But TR = TS + SR
 =
= 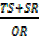
=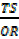 +
+ 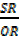 , but TS = PQ
, but TS = PQ
= +
+ 
Multiplying 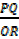 by
by  and
and 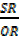 by
by 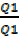

But from the figure above
 =
= 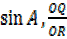 =
= 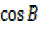
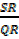 =
= 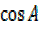 ,
, 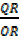 =
=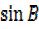
Then substituting into
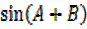 =
=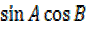 +
+ 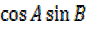

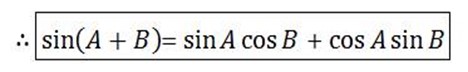
From (1) if B=–B
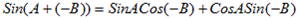
But  =
=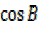
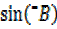 =â»
=â»
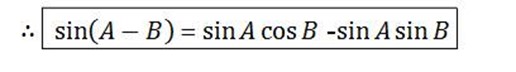
Again from the figure above 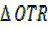
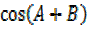 =
=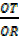
But OT =  –
– 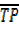

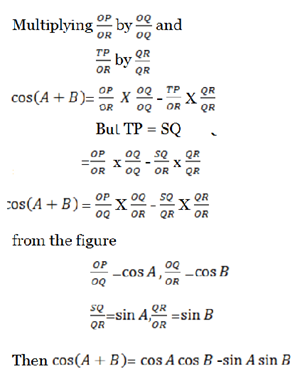

For tan 
Refer 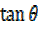 =
=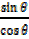
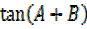 =
=
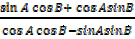
Dividing numeration and denomination by 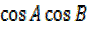
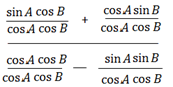
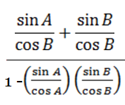
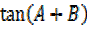 =
=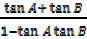
From above equation
If B = -B, then
Tan( A+ =
= 
But tan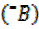 =â» tanB
=â» tanB
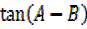 =
=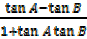
Or, shown by
 =
= 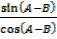
Use procedure (5) obtain (6)
APPLICATION OF THE COMPOUND FORMULAE
I. PROVING OF IDENTITIES
Examples:
Prove the following trig identities
i) 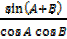 =
= 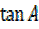 +
+ 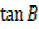
ii)  =
=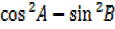
iii) 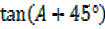 =
=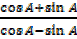
Proof(i) 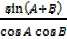 =
=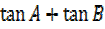
Dealing with L.H.S
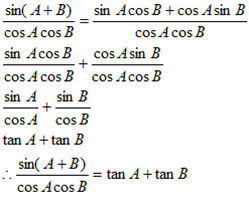
II. COS(A+B)COS(A-B) =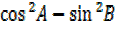
Proof dealing with L.H.S 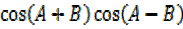
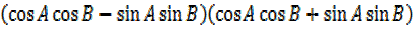
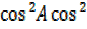 B –
B – 
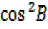 =1-
=1- 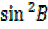 and
and
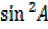 = 1 –
= 1 –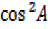 then
then
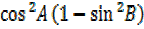 –
– 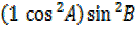
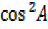 –
–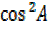
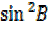 -(sin2A-cos2Asin2B)
-(sin2A-cos2Asin2B)
cos2A-cos2Asin2B-sin2A+cos2Asin2B
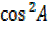 –
– 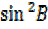 R.H.S
R.H.S
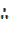
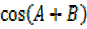
 =
=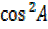 –
–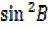
III. 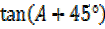 =
=
Proof
Dealing with L.H.S
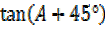 =
=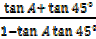
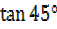 =1
=1
=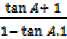
But  =
= 
=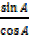 + 1
+ 1
1 – 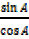
=
= 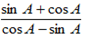
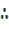
 =
=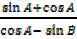
IV. FINDING VALUES OF TRIG RATIOS
Examples: Evaluate
a) 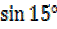 b)
b) 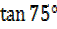 c)
c) 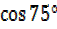 d)
d) 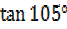
Solution:
a) 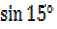 =
= 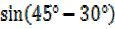
=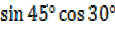 –
– 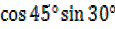
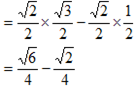
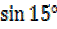 =
=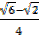
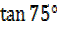 =
=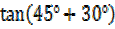
= 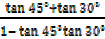
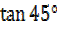 = 1
= 1
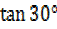 =
=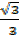
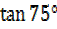 =
= 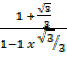 =
= 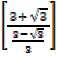
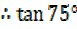 =
= 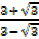
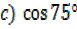 =
= 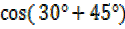
=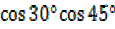 –
– 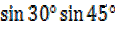
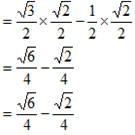
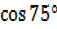 =
= 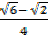
 .
.
If 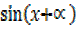 =
= 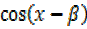 , find the tangent of x in terms of
, find the tangent of x in terms of 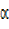 and
and 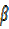 then find tan x when
then find tan x when 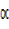 = 45° and
= 45° and  = 60° (leaving your answer in surd form)
= 60° (leaving your answer in surd form)
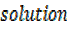 :
:  = cos
= cos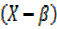
 +
+ 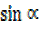 =
= 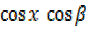 +
+ 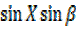
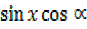 –
– 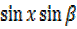 =cos x cos
=cos x cos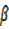 –
–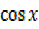 sin
sin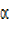
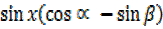 =
=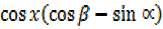
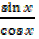 =
= 
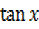 =
=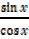 =
= 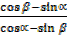
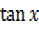 =
=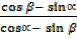
Given 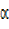 =45°,
=45°, 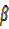 = 60
= 60
 =
= 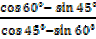
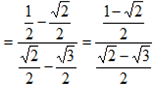
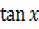 =
= 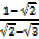
DOUBLE ANGLE FORMULAE
Recall (a) 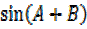 =
=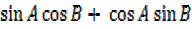
If B = A
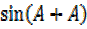 =
= 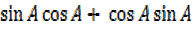
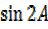 =2
=2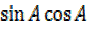
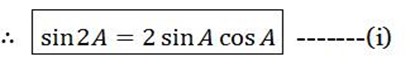
b) 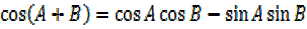
If B = A
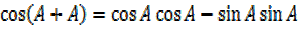
= 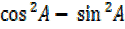


c) 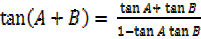
If B = A
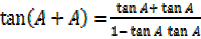
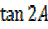 =
=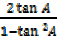 ………………….. (iii)
………………….. (iii)
Also from
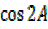 =
=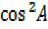 –
–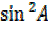
But 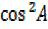 = 1 –
= 1 –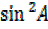
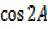 =(1 –
=(1 –
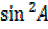 )-
)- 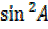
= 1 –
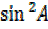 –
– 

Or
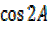 =
= 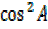 –
– 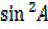
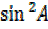 = 1 –
= 1 – 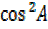
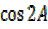 =
=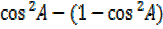
= 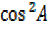 – 1 +
– 1 + 
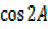 = 2
= 2 – 1
– 1
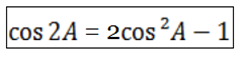
TRIPLE ANGLE FORMULAE
i) Consider 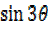
sin(2θ+θ) =sin2θcosθ +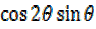
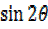 = 2
= 2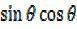
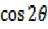 =
=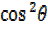 –
– 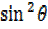
 = 2
= 2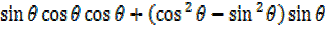
= 2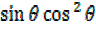 +
+ 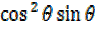 –
– 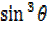
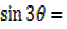 3
3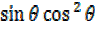 –
– 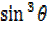
But 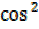 θ = 1 –
θ = 1 –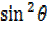
=  –
–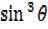
= 3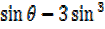 θ –
θ – 
=3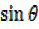 – 4
– 4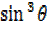

ii) Consider 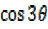 =
= 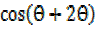
=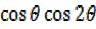 –
– 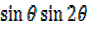
But  =
= 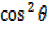 –
– 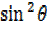
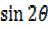 = 2
= 2
=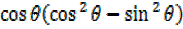 –
–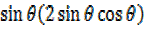
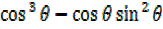 -2
-2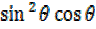
 =cos3θ
=cos3θ
But 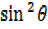 =1 –
=1 –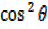
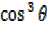 – 3
– 3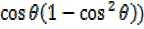
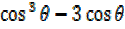 +3
+3
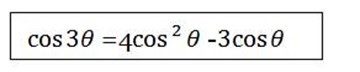
iii) Consider 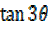
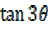 =
=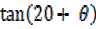
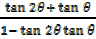
But  =
= 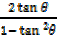
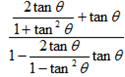
=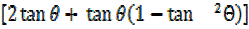

=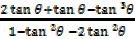

Alternative: Using 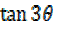 =
=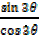
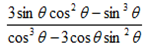
Dividing by cos3θ numerator and denominator