Applications of the double and triple formulae
A. Proving Identities
Examples: Prove the following identities
(i) 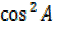 +
+ 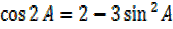
(ii)  =
= 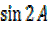
(iii) 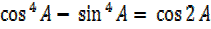

Solution(i)
I. Proof 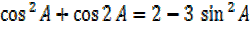
Dealing with L.H.S

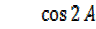 =
=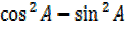
=cos2A+cos2A-sin2A
=2cos2A-sin2A
 –
–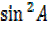
=2 – 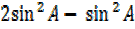
=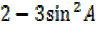 R.H.S
R.H.S
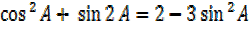
II. Solution(ii)

Dealing with L.H.S
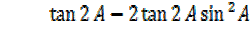
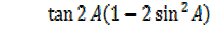
But 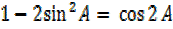
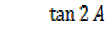
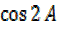
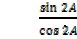
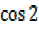 A =
A =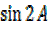 R.H.S
R.H.S
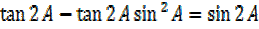
III. Solution(iii)
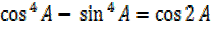
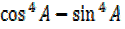 =
=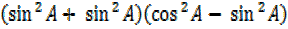
= 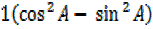
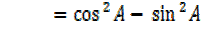
=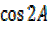
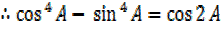
Work on the following problems prove the identities
i) 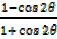 =
= 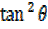
ii) 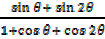 =
=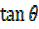
iii) 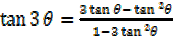
iv) 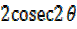 =
=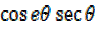
v) 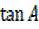 +
+ 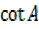 =2
=2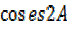
vi) 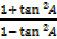 =
=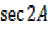
vii) 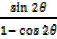 =
= 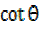
viii) 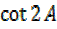 =
= 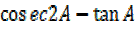
ix) 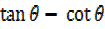 = 2
= 2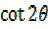
x) 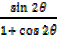 =
= 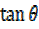
xi) 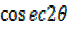 +
+ 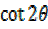 =
=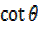
Warm up with:
i) Find tan  without calculate mathematical tables
without calculate mathematical tables
ii) 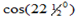
HALF ANGLES FORMULAE
From 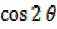 =
=  –
– 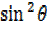
Then 
= 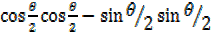
=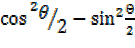
=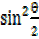 = 1 –
= 1 – 
=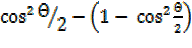
=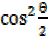 – 1 +
– 1 +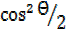
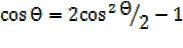
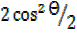 =
= 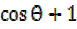

Again from  =
= –
– 
But 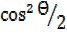 = 1 –
= 1 –
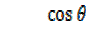 =1 –
=1 –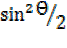 –
– 
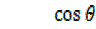 = 1 -2
= 1 -2
2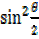 = 1 –
= 1 –
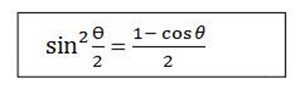
For 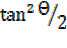 =
= 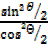
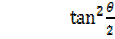 =
=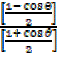 =
= 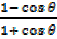

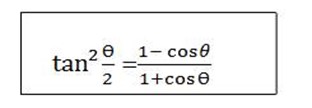
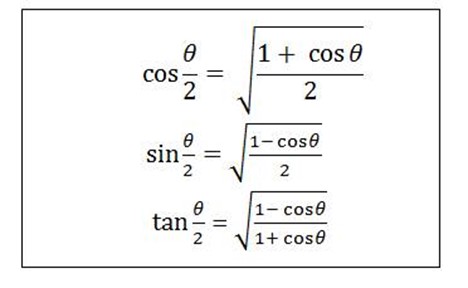
Similarly the formulae can be expressed as
EQUATION OF THE FORM
a 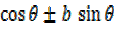 = c
= c
where a, b and c are real constant.
The task here is to solve the equation. The are two ways to solve.
i. Using t –fomulae
ii. Using R – fomula (or transforming a function a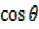 + b
+ b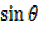 = c as a single function)
= c as a single function)
I. USING t- FORMULAE
Consider 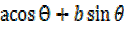
Concept of t formulae From 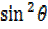 =
= 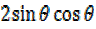
=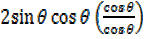
=
=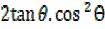

But 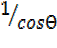 =
= 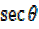
= 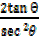
Again  = 1 +
= 1 + 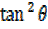
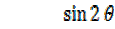 =
=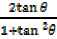
Let 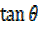 = y
= y
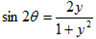
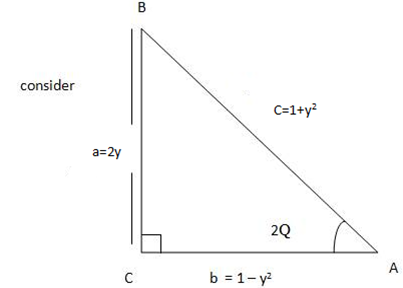
from Pythagoras theorem
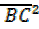 +
+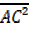 =
= 
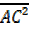 =
=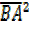 –
– 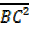
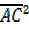 = (1+y2) –
= (1+y2) – 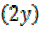 ²
²
=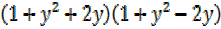
=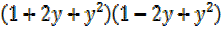
=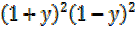
= 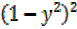
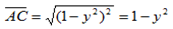
Then 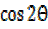 =
= 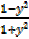
Cos2ÆŸ = 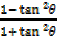 …………………… (ii)
…………………… (ii)
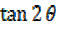 =
=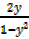 =
= 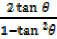
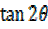 =
= 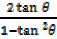 ………………………..(iii)
………………………..(iii)
From equations (i) (ii) and (iii) it follows that
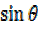 =
=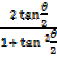
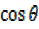 =
=
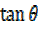 =
= 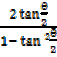
Let t = , then we get
, then we get
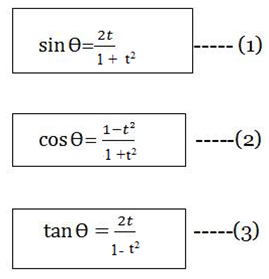
Equation (1), (2) and (3) are called t-substitution formulae
Solving the equation
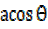 + b
+ b  = c
= c
Let t =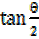
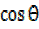 =
= ,
, 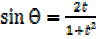
 + b
+ b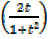 = c
= c
 =c
=c
a – at² + 2bt = c(1 + t²)
a – at² + 2bt = c + ct²
at² + ct² – 2bt + c – a =o
(a + c)t² – 2bt + c –a =o
Quadratic equation
Solve for it
t= 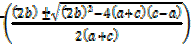
= 
=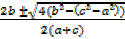
= 
t = 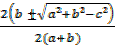
= 
t = 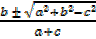
but t = 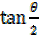
tan =
= 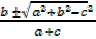
 =
= 
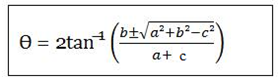
Example:
Solve for values of θ between 0° and 180° if 2cos θ+ sin θ= 2.5
Solution: let t = tan 
2 + 3
+ 3  =2.5
=2.5
Then  =
= 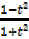
Sin θ= 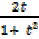
2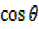 + 3
+ 3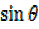 2.5
2.5
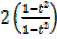 + 3
+ 3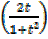 = 2.5
= 2.5
2 -2t² + 6t =2.5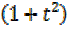
2– 2t² + 6t = 2.5 + 2.5t²
2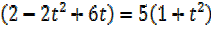
4– 4t² + 12t = 5 + 5t²
9t² – 12t + 1 = 0
t= 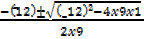
= 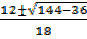
= 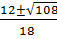 =
= 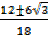
= 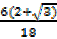
=
t = 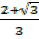 = 1.244 or t =
= 1.244 or t =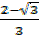
t = 0.00893
case 1:
t =1.244, t= tan tan
tan = 1.244
= 1.244
 = tan
= tan 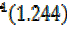
 =
=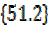
 =51.2° = θ = 51.2 x 2
=51.2° = θ = 51.2 x 2
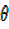 = 102.4°
= 102.4°
case 2:
t = 0.0893
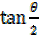 = 0.0893
= 0.0893
 =
= 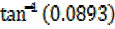
 =
= 
 =5.1°, θ = 10.20
=5.1°, θ = 10.20
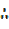 θ=
θ=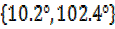
Example 2: solve the equation
5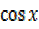 – 2
– 2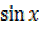 =2 for
=2 for
for -1800
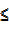 x
x 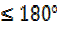
Using t formula, let t = 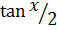
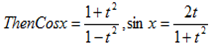
5cosx – 2sin x=2
5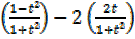 =2
=2
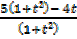 =2
=2
5 – 5t² -4t = 2
5 – 5t² – 4t = 2 + 2t²
7t² + 4t -3 =0
7t² + 7t – 3t -3 =0
7t (t + 1) -3(t + 1) =0
(7t – 3) (t + 1)=0
7t – 3 = 0 or t + 1=0
7t =3 t= -1
t = 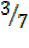
Case 1.
t=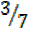 = 0.42857
= 0.42857
 = 0.42857
= 0.42857
 =
= 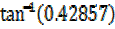
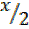 = 23.2° = 23.2°x2=46.4°
= 23.2° = 23.2°x2=46.4°
Case2,
t=–1, tan 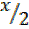 = â»1
= â»1
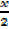 =
= 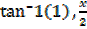 =
= 
II. SOLVING THE EQUATION
acosθ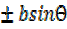 = C
= C
R-formula or simply transforming a function acosÆŸ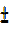 bsinÆŸ as a single function.
bsinÆŸ as a single function.
From acosθ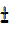 bsinθ = c
bsinθ = c
Consider acosθ + bsinθ – this can be expressed transformed into form

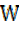 here R >O
here R >O
R is the maximum value of a function (or Amplitude)
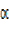 is a phase angle and it is an acute angle
is a phase angle and it is an acute angle
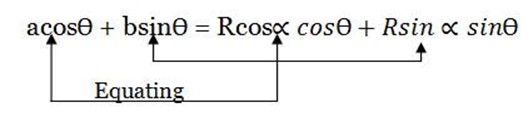
Then from acosθ + bsinθ =C
acosθ + bsinθ = Rcos(θ –  )
)
acosθ + bsinθ= R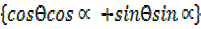
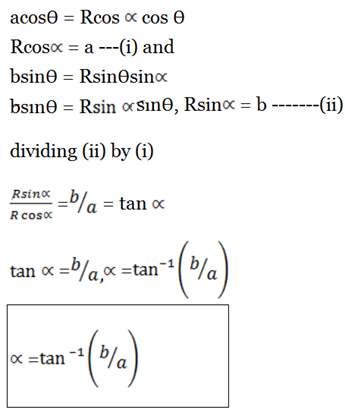
Square equation (i) and (ii) then sum
(Rcos +
+  = a² + b²
= a² + b²
R²cos²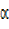 + R²sin²
+ R²sin²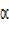 = a² + b²
= a² + b²
R²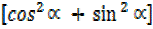 = a² + b²
= a² + b²
But 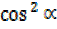 +
+ 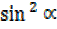 =1
=1
R².1 = a² + b²
R² =a² + b²
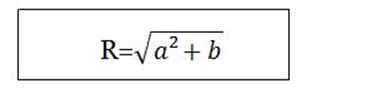
Then from
acosÆŸ + bsinÆŸ =c = Rcos (ÆŸ – 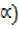
Rcos(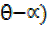
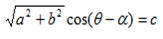
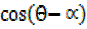 =
=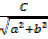
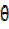 –
–  =
= 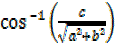
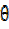 =
=
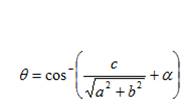
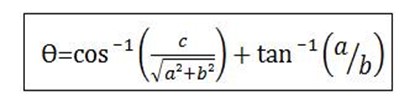
Example

Rcos 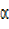 cosx = 3cosx
cosx = 3cosx
Rcos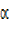 = 3 —- (i)
= 3 —- (i)
-4sinx = Rsinxsin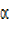
Sin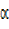 = 4 —– (ii)
= 4 —– (ii)
Dividing (ii) by (i), then we get
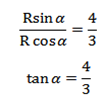
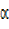 =
= 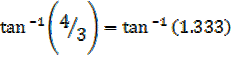

 (i) and (ii) then sum
(i) and (ii) then sum
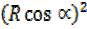 +
+ 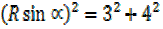
= 9 + 16
R²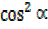 + R
+ R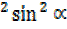 = 25
= 25
R²1 =25
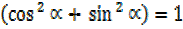
R= 25, R=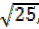 R=5
R=5
But 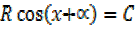
5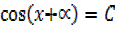
C = 1.5 , 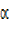 = 53.12°
= 53.12°
5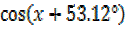 = 1.5
= 1.5
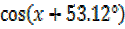 =
= 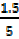
Cos 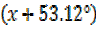 =0.3
=0.3
X + 53,12°= 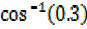
X + 53.12° = 72.54°
X = 72.54° – 53.12°
 x = 19.42°
x = 19.42°
Example 2: solve for 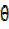 between 0° and 180° if
between 0° and 180° if
2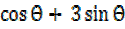 = 2.5
= 2.5
Solution
2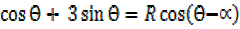 = 2.5
= 2.5
R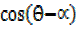 =2
=2 3
3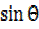
R
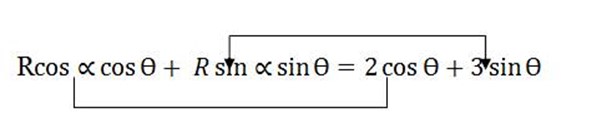
R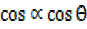 =2
=2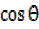
R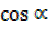 =2 —(i) and
=2 —(i) and
R
R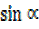 = 3 ………. (ii)
= 3 ………. (ii)
Dividing (ii) by (i)
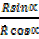 =
= 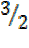
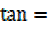
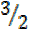 ,
, 
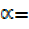
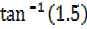 = 56.3°
= 56.3°
Squaring (i) and (ii) then add
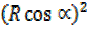 +
+ 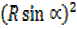 = 2² + 3²
= 2² + 3²
R²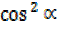 + R
+ R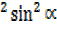 = 4 + 9
= 4 + 9
R²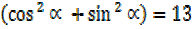
R² = 13, R=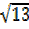
Then 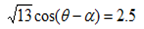
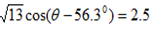
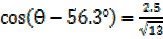
θ- 56.3°= 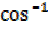
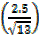
θ= 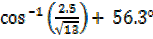
=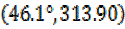 + 56.3°
+ 56.3°
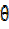 = 46.1° + 56.4°= 102.4°
= 46.1° + 56.4°= 102.4°
θ= 313.9° + 56.3°= 370.2°
= 370.2° – 360°=10.2°
 θ=10.2°,102.4°
θ=10.2°,102.4°
Example: 3
solve for x iƒ5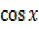 – 2sinx =R
– 2sinx =R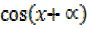 =2
=2
5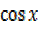 – 2
– 2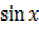 = R
= R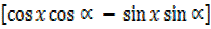
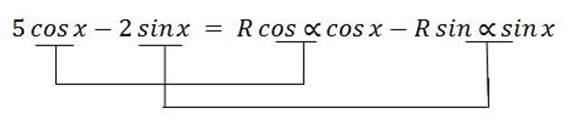
5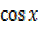 = R
= R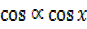
R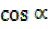 = 5 ……………………. (i)
= 5 ……………………. (i)
2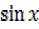 = R
= R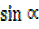
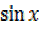
R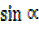 = 2 ……………………..(ii)
= 2 ……………………..(ii)
Dividing (ii) by (i)
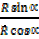 =
= 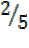 ,
,  =
= 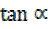 =
= 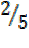
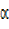 =
= 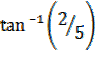 =
= 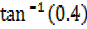 =21.8°
=21.8°
Squaring equations (i) and (ii) the add
 2² + 5²
2² + 5²
R²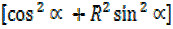 = 29
= 29
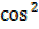
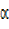 +
+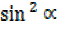 = 1
= 1
R²x1 =29, R²=29, R = 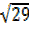
From R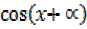 = 2
= 2
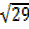
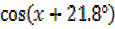 = 2
= 2
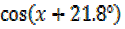 =
= 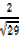
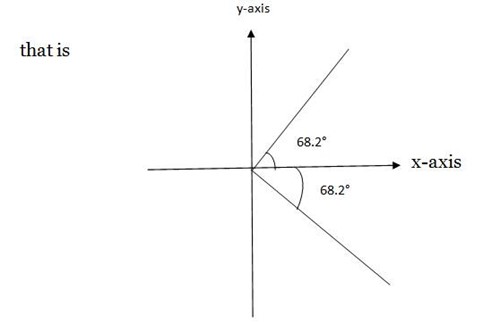
X + 21.8 = 
X + 21.8° = 68.2° , -68.2°
X= 68.2° – 21.8° = 46.40°
Also x + 21.8° = â»68.2°
X = â»68.2° -21.80 =-90
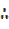 x =
x = 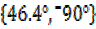
NB: The R- formula ( Transformation) can also be done using an auxiliary angle approach; where we substitute constants a and b as functions of sine or cosine.
Thus considering the same problem solving 5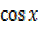 – 2
– 2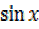 =2
=2
Imagine a triangle
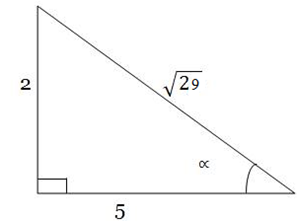
Using Pythagoras theorem
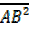 =
= 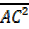 +
+ 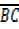 ²
²
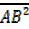 = 5² + 2² = 25 + 4 = 29
= 5² + 2² = 25 + 4 = 29
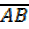 =
= 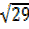
From the figure above, it follows that
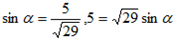
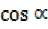 =
= 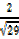 , 2 =
, 2 = 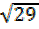 cos
cos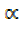
Then from 5cos x – 2sin x = 2
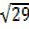
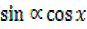 –
–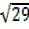
 = 2
= 2

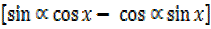 = 2
= 2
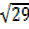
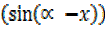 =2
=2
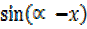 =
= 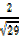
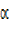 – x =
– x = 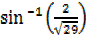
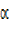 -x = 21.8°
-x = 21.8°
So, the principle angle = 21.8°

Using the general solution of sin
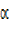 – x = 21.8°, thus 180°n +
– x = 21.8°, thus 180°n + 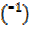 n
n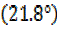
 = 68.2°
= 68.2°
X =  – 21.8°
– 21.8°
X = 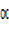 –
–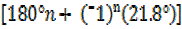
X= 68.2° – 
n= 
find x values according to the limits given in the question
OR imagine a triangle
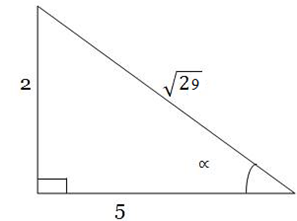
Then sin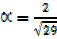 , 2=
, 2=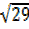 sin
sin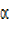
cos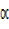 =
=  , 5=
, 5= 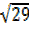 cos
cos 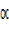
from 5cosx – 2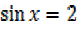
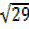
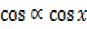 –
– 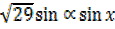 = 2
= 2
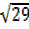
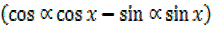 = 2
= 2
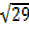
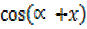 =2
=2
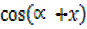 =
=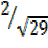
 + x =
+ x =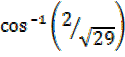 =68.2°
=68.2°
Using the general solution of cosine

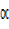 + x =360°n
+ x =360°n 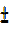 68.2°
68.2°
X = 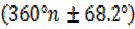 –
–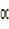
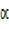 = 68.2°
= 68.2°
X=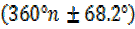 – 21.8
– 21.8
n =