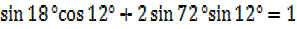OTHER KIND OF QUESTIONS USING THE TRANSFORMING INTO A SINGLE FUNCTION CONCEPT
Example:1 Express
i) 4cosx – 5sinx in the form of Rcos(x + 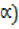
ii) 2sinx + 5cosx in the form of Rsin(x + 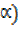
Solution(i)
4cos x-5sinx =Rcos(x + 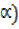
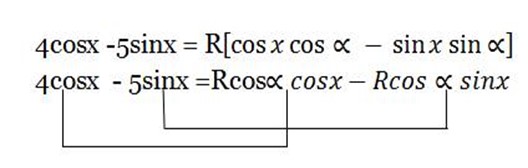
4cosx = Rcos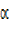 cosx
cosx
Rcos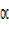 = 4 ……… (i)
= 4 ……… (i)
5sinx = Rsin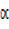 sinx
sinx
Rsin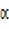 =5 …………..(ii)
=5 …………..(ii)
Dividing (ii)by (i)
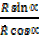 =
= =
= 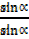 = tan
= tan 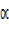
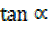 =
=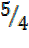
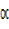 = tan⻹
= tan⻹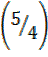
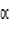 =
=
Squaring equations (i) and (ii) then add
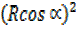 +
+ 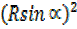 = 4² + 5²
= 4² + 5²
R²cos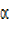 + R²
+ R²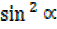 = 16 + 25
= 16 + 25
R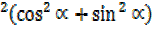 = 41
= 41
R=41, R=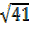
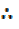 4cos x -5 sin x =
4cos x -5 sin x = 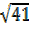 cos(x+ )
cos(x+ )
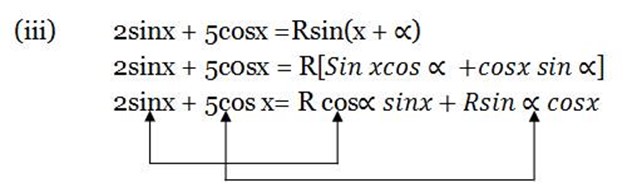
Rcos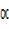 sinx = 2sinx
sinx = 2sinx
Rcos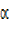 =2 …………(i) and
=2 …………(i) and
Rcosxsin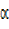 = 5cosx
= 5cosx
Rsin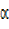 = 5 ………….(ii)
= 5 ………….(ii)
Dividing (ii) by (i)
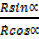 =
= 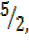
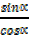 =
= 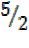
Tan 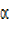 = ,
= , 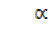 =
= 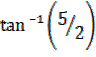
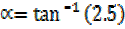
Squaring equations (i) and (ii) then add
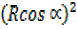 +
+ 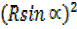 = 2² + 5²
= 2² + 5²
R²cos²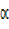 + R² sin²
+ R² sin²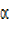 = 4 + 25
= 4 + 25
R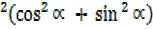 =29
=29
But cos²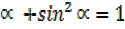
R²(1)=29
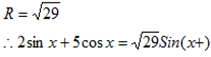
Example. Find the maximum value of 24sinx -7cosx and the smallest positive value of x that gives this maximum value.
Solution. 24sin x -7cosx = Rsin(x – 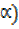

24sinx = Rcos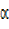 sinx
sinx
Rcos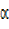 =24, 7cosx = Rsin
=24, 7cosx = Rsin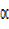 cosx
cosx
Rsin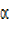 =7 ………(ii)
=7 ………(ii)
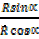 =
= 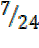
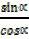 =
= 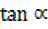 =
=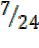
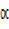 =
=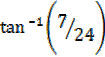 = 16.26°
= 16.26°
Squaring equation (i) and (ii) then add
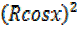 +
+ 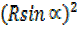 =
=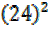 +
+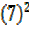
R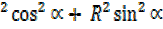 =625
=625
R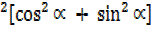 =625
=625
R²=625, R=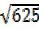
R =25
24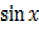 – 7cosx = Rsin
– 7cosx = Rsin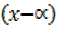
=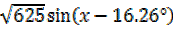
=25sin 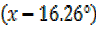
24sinx – 7cosx = 25sin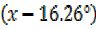
f(x)= 25sin(x – 16.26°)
Max value of sine function is when
Sin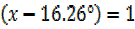
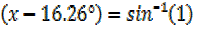
X – 16.26°=90°
X = 90° + 16.26°
X= 106.26°
Hence max value f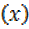 =y=25 sin 90°
=y=25 sin 90°
=25
 The maximum value is 25 obtained when x = 106.26°
The maximum value is 25 obtained when x = 106.26°
Note. The maximum values of
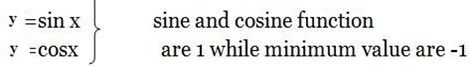
Problems to work on
Using t formula and R –formula solve the following.
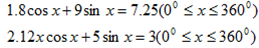
3. 6sinx + 8cosx =6
4. Express 7cosθ+ 24 sinθ in the form of Rcos(10 –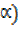
5. Solve for θ
3cosθ + 4sinθ =2
6. 5cos2θ– sin 2θ=2
Note: If the question has no limits/boundaries write the answer using the general solution
FACTOR FORMULAE (SUM AND DIFFERENCE FORMULAE)
The concept here is to express the sum or difference of sine and cosine functions as product and vice versa
Refer
Sin(A +B) = sin AcosB + cosAsin B ……….(i)
Sin(A –B) = sinAcosB –cosAsinB ………….(ii)
Cos(A + B) =cosAcosB – sinA sinB …………(iii)
Cos(A+ B) =cosAcosB + sinAsinB ……………(iv)
Add (i) and (ii)
Sin(A + B) + sin(A +B) =2sin AcosB
Let f = A + B ………(i)
Q =A-B …….(ii)
(a) +(b) 2A = P+Q, A= 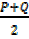
(a) –(b) 2B =P-Q, B=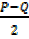
Therefore sin(A+B)+sin(A-B)=2sinAcosBbecome
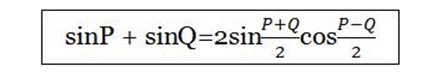
SinP + sinQ= 2sin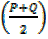 cos
cos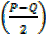 …(1)
…(1)
Substract(i) –(ii)
Sin(A+B) –sin(A-B) = 2cosA sinB
But P=A+B, Q=A-B
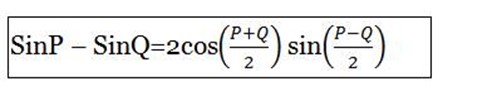
Add (iii) and (iv)
Cos(A+B)+cos(A-B) = 2cosAcosB
CosP + cosQ = 2cos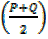 cos
cos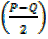
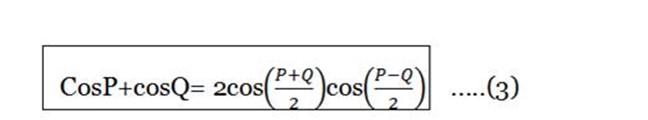
Substract (iii) – (iv)
Cos(A + B) –cos(A-B) = -2sinAsin B
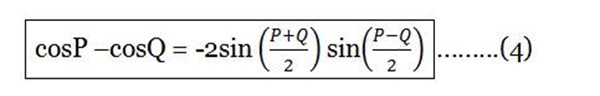
Expressions (1) (2) (3) and ( 4) are called factor formulae
APPLICATIONS OF THE FACTOR FORMULAE
a) Proving problems
Examples
i) 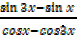 = cot 2x
= cot 2x
ii) 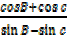 = cot
= cot 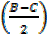
iii) 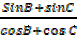 = tan
= tan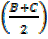
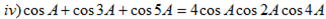
v) If A, B and C are angles of a triangle prove that
cosA +cosB + cosC -1 = 4sin 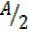 sin
sin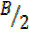 sin
sin 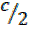
vi) If A, B and C are angles of a triangle prove that
cos2A + cos2B + cos2C + 1 = 4cosAcosBcosC
vii) 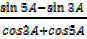 =tan A
=tan A
viii) 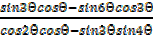 =
=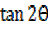
Solution (i)
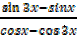 (L.H.S)
(L.H.S)
= 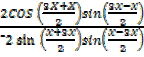
= 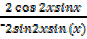
But 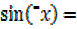 –
–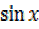
= 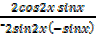
= 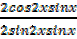 =
= 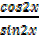
= 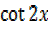
= 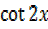
Solution(ii)
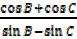 ,
,
= 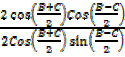
= 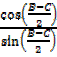
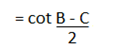
Solution (iii)
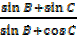 =
= 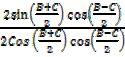
= 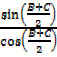 R.H.S
R.H.S
=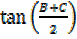
Solution(iv)
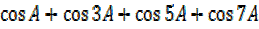 = 4
= 4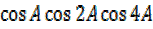
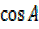 +3A = 2
+3A = 2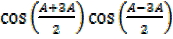
=2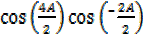
=2cos2Acos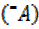
=2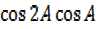
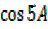 +
+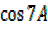 =2
=2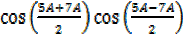
=2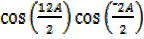
=2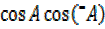
=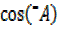 =
=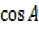
=2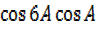
Then
=2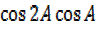 + 2
+ 2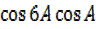
=2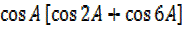
=2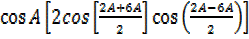
=2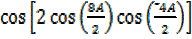
=2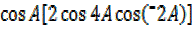
=2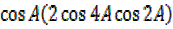
=4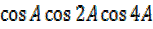 R.H.S
R.H.S
Solution(V).
A, B, C are angles of a 
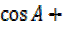
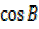 +
+ 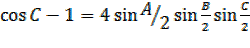
L.H.S
CosA + cosB + cosC – 1
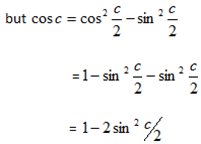
2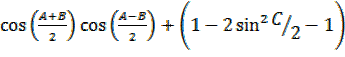
=2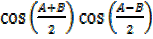 -2
-2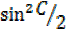 ………….(i)
………….(i)
But A + B + C= 180°
(Degree angle in 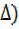
A + B = 180°-C
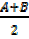 =
=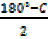
90 –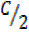 =
= 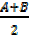
Apply cos
cos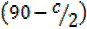 = cos
= cos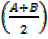
Cos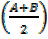 =
= 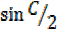
2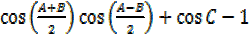
But 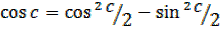
=1 –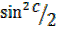 –
–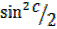
= 1 – 2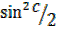
Substitute (ii) into (i)
=2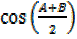 cos
cos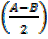 -2sin
-2sin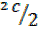
= 2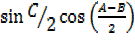 -2
-2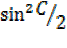
=2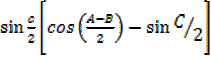
=2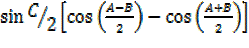
But 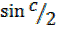 =
=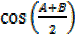
Using factor formula
2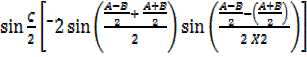
2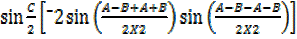
2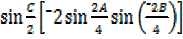
2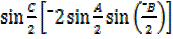
But 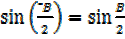
2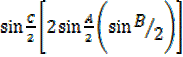
2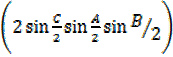
=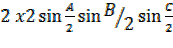
=4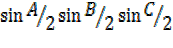
solution(VI).
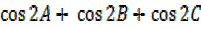
= 4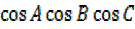
From factor fomulae
=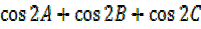
=2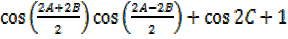
=2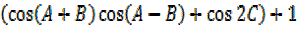
But A + B +C = 180° (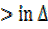 )
)
A +B = 180° -C
Cos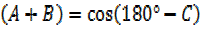
=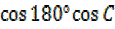 +
+ 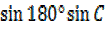
= –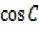 + 0
+ 0
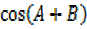 = –
= –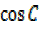
Substitute into (i)
=-2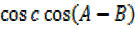 +
+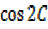 + 1
+ 1
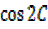 =
=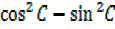
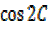 =
=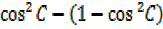
=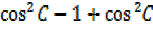
=2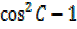
= -2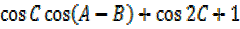
= -2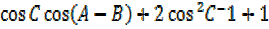
= -2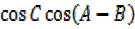 +2
+2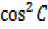
=2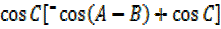
But = –
= –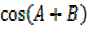
2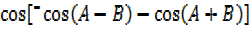
= -2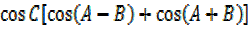
= -2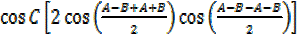
= -2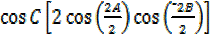
= -2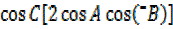
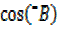 =
=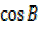
= -4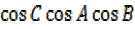
=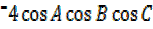
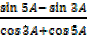 =
=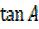
=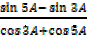
=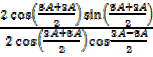
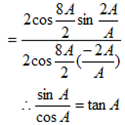
Solution (vi)
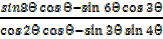
L.H.S changing the products into sin or difference
Numerator: 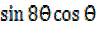
From sinP +sinQ=2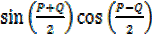
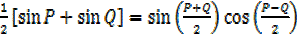
= 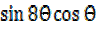
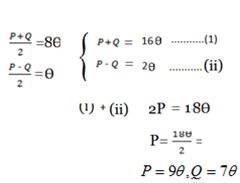
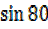
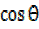 =
= 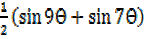
Similarly 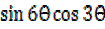 =
=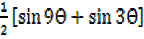
Denominator
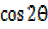
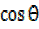 =
=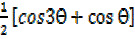
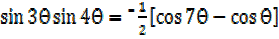
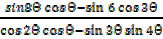
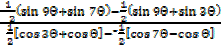
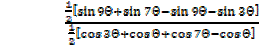
=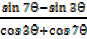
=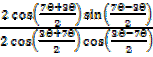
=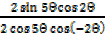
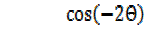 =
=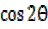
=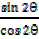
=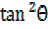 RHS
RHS
Examples (i) solve for x if
 +
+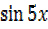 =
=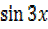 for 0°
for 0°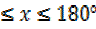
ii) 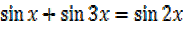
For 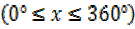
iii) 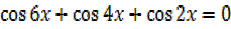
For 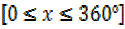
Solution (i)
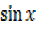 +
+ 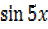 =
=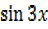
Writing using factor formulae
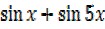 =2
=2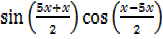
=2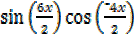
=2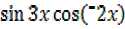
=2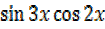
2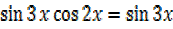
2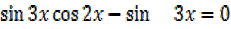
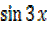
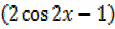 =0
=0
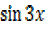 =0, 2
=0, 2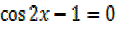
2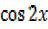 =1
=1
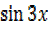 =0
=0 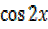 =
= 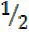
3x = 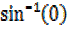 =0°, 180, 360°
=0°, 180, 360°
X= 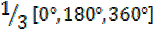 540°
540°
=0°,60°,120°, 180°
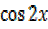 =
=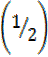 = 60°,300°
= 60°,300°
X= 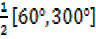
X=30°, 150°
 x=
x=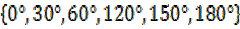
iv) 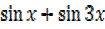 =
=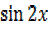
2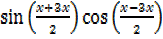 =
=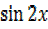
2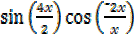
2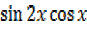 =
=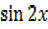
2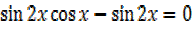
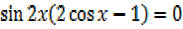
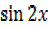 =0, 2
=0, 2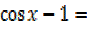 0
0
2x=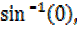 2
2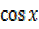 =1
=1
2x=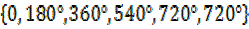
X=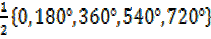
X=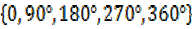
X= 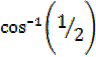
X=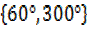
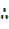 x=
x=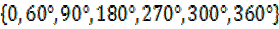
Questions
1. Solve for the value of x between 0° and 360° in the question
i) 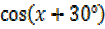 –
– 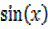 =
= 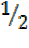
ii) 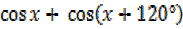 +
+ 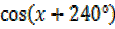 =0
=0
2. Prove that
i) 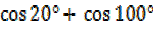 +
+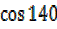 °=0
°=0
ii) 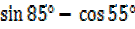 =
=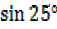
3. Simplify 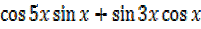
4. Evaluate 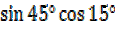
5. Prove that
2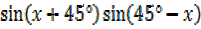 =
=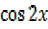
If 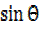 +
+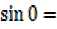 a and
a and
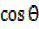 +
+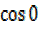 =b show that
=b show that
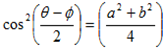
7. Prove that
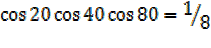
8. Express as a sum or difference
i) 2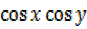
ii) 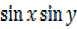
iii) 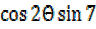 θ
θ
iv) 2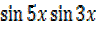
9. Show without using tables or calculators
i) 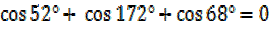
ii) 2