RADIANS
Definition
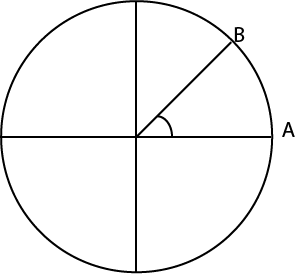
1 radian is an angle subtended at the centre of the circle of the circle by an are equal in length to that radius.
i.e
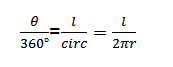
But θ = 1 radian
Circumference = 2 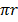
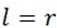
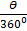 =
= 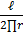
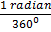 =
=  =
=  =
= 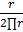
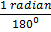 =
= 
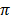 Radian = 180o
Radian = 180o
Note: It is customary to omit the unit radian
 = 180o
= 180o
Exercise 1.3
1. Convert the following into degrees
a) 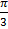 b)
b) 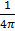 c)
c) 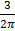 d)
d) 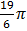
e) 5 f) g)
g) 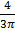 h)
h) 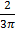
j) 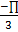
2. Convert the following into radians
a) 120o b) 4o c) -90o d) 15o
e) 60o f) 240o g) -315 h) -90o
i) 357o j) 300o k) -630o
3. Solve for x such that 0o ≤ x ≥ 360o
a) Cos x = -1
b) Cos x = –
c) Sin x = – 
d) Sin x = 0
e) Cos x = 
f) Sin x = 
g) Tan x = undefined
h) Tan x = 0
i) Tan x = -1
j) Tan x = 1
4. Evaluate sin θ if the terminal side of θ contains the given point
a) P (10, -4) b) P (3, 4) c) P (3, -5) d) P (-1, 3)
e) P (-8, -13)
5. If cos θ = -2/5 and sin θ < 0, find sin θ
6. If cos θ = 5/3 and sin θ < 0, find sin θ.
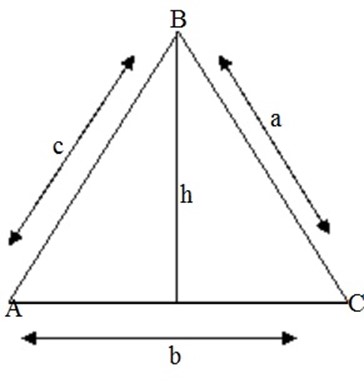
 Sin A = h/c h=c sin A
Sin A = h/c h=c sin A
 Sin C = h/a h=a sin C
Sin C = h/a h=a sin C
Sin A / a = sin C / c
Similarly, by drawing the altitude from A to BC.
b sin C = c sin B
Sin C / c= sin B / b
Hence; sin A /a = sin B / b = sin C / c
It is called the sine rule.
Note:
a) When two angles and one side of any triangle are known, the sine rule can be used to solve the triangle
b) When two sides and an angle opposite to any of the two given sides are known, the sine rule can be used to solve the triangle.
Example
7. In triangle ABC, B = 390, C = 820, a = 6.73 cm find C
Solution
From 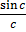
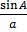
= 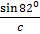 =
= 
But A = 180o – (39o + 82o)
= 59o
= 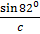 =
= 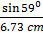
C = 6.73cm x 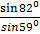 = 7.78 cm
= 7.78 cm
Example 1.4
Find the remaining angles of the AABC in which a = 12.5 cm , c = 17.7 cm and C = 1160
Solution
 =
=  =
= 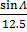 =
= 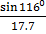
= sin A = 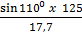
A = sin-1(0.6347)
A = 390.24
B = 180o – 155 = B = 24o 36
Exercise 1.5
1. Solve completely the triangles in which
a) b = 6m, A= 80o, C = 46o
b) A = 50o, B = 60o, a = 4m
c) a = 400m, A = 31o20, B = 70o40
d) A = 115o, a = 65m, b = 32m
Cosine rule
Consider the triangle ABC
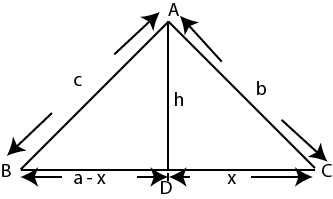
By using Pythagoras theorem
C2 = (x – a) 2 + h2
C2 = x2 – 2ax + a2 + h2
C2 = x2 + h2 + a2
C2 = a2 + b2 – 2ax
But 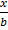 = cosC
= cosC
C2 = a2 + b2 – 2ab Cos C
For angle B
b2 = a2 + c2 – 2ac Cos B
For angle A
a2 = b2 + c2 – 2bc Cos A
Note
a) When two sides and an angle between the two sides are included then the angle between the two lines of the cosine rule can be used to solve the triangle by using the cosine rule.
b) We can also solve the triangle by cosine rule if all the three sides are given
Example 1.6
Given a triangle with a = 50cm, c =60cm, and B = 100o .Find b
Solution
b2 = a2 + c2 – 2ac Cos B
= (50) 2 + (60) 2 – 2 (50) (60) Cos 100o
= 3600 + 2500 – 6000 (-0.1736)
= 7141.6 cm
Example 1.7
Given a = 8cm, b = 5cm, and c = 4cm, find the smallest and largest angles.
Solution

i) To find A we use
a2 = b2 + c2 – 2bc Cos A
64 = 25 + 16 – 40 Cos A
40cos A = 41 – 64
40cos A = -23
Cos A = 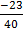 = -0.5750
= -0.5750
A = 125o10
ii) To find C we use
c2 = a2 + b2 – 2abCos C
16 = 82 + 25 – 2 (8) (5) Cos C
16 = 64 + 25 – 2(8)(5)Cos C
80cos C = 89 – 16
Cos C = 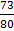 = 0.9125
= 0.9125
C = 24o10
Trigonometric identities
Figure 8.15 show the right angled triangle with sides a, b, c and angles A, B, C
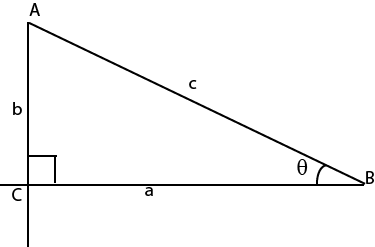
By the use of Pythagoras theorem
a2 + b2 = c2
Divide throughout by c2
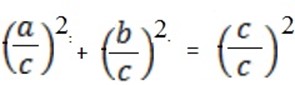
But  = cos θ,
= cos θ,  = sin θ
= sin θ
Cos2 θ + sin 2 θ = 1
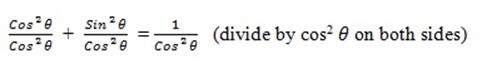
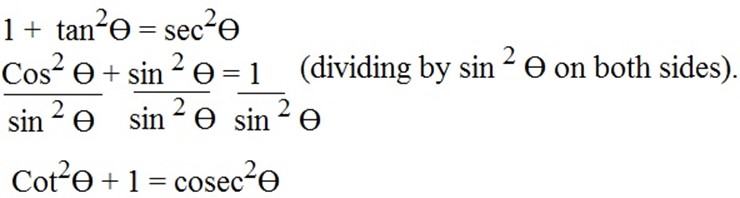
Exercise 1.8
1. Use the cosine rule to solve the following triangles
a) A = 60o, b = 3cm, c = 4cm
b) A = 100o, b = 8cm, c = 10cm
c) A = 50o, b = 5cm, c = 8cm
d) a = 9cm, b = 10, C = 120o
e) a = 5, b = 10, c = 1200
f) a = 10cm, b = 20cm, c = 120cm
2. Find the largest and smallest angles of triangle whose side area a= 5cm b = 10cm and c = 12cm
3. Two people are on opposite sides of a hill and are 600m apart. If the angles of elevation from these people to the top of the hill are 19o and 21o, how high is the hill?