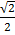BAM FORM 6 – TRIGONOMETRY

 

Compound Angles

The formulae that follow are the ones we refer to as the compound angles

Sin (A + B) = sin A Cos B + Cos A sin B

Sin (A – B) = sin A Cos B – Cos A sin B

Cos (A + B) = Cos A Cos B – sin A sin B

Cos (A – B) = Cos A Cos B + sin A sin B

Solution

Sin (A + B) =  Sin A Cos B + Cos A Sin B

Holder the area of the triangle RST

                             

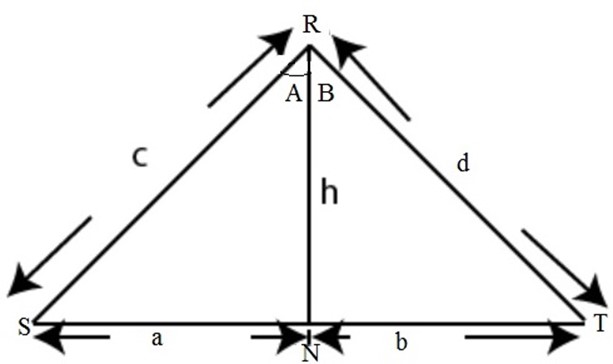
Area (ΔRST) = area (ΔRNS) + area (ΔRNT)

 cd sin (A + B) =  hc sin B +  hd sin B

Multiplied throughout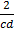

Sin (A + B) =  sin A +  sin B

But  = cos B and  = cos A

            Sin (A + B) = sin A Cos B + Cos A sin B

Cos (A + B)

Apply the cosine rule on the same triangle in figure 8.16

(a + b) ² = c² + d² – 2cd Cos (A + B)

     

                                    =

                                    = 

                                   =

                                    =

                                    =

                                    =   – 

                                    =  .

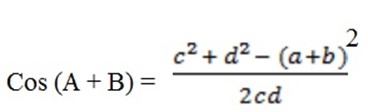
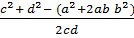
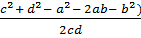
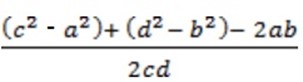
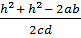
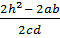
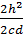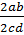
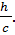
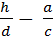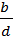
                                    =   = Cos A and  = cos B

                                    =  = sin A and   = sin B

                        Thus,

                        Cos (A + B) = Cos A Cos B – sin A sin B

            Sin (A – B)

            Consider the area of triangle RST

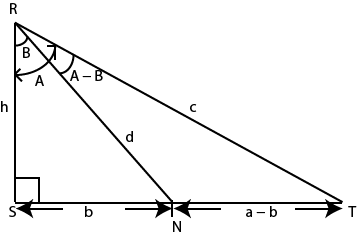
                        Area (ΔRNT) = area (ΔRST) – area (ΔRSN)

             cd sin (A –B) =  hc sin A –  hd sin B

            Multiplied throughout by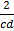

            Sin (A – B) =  ,  sin A – sin B

            But   = cos B,   = cos A

                      Sin (A – B) = Cos B sin A – Cos A sin B

            Cos (A – B) use the same figure and apply the cosine rule (a – b) ² = c² +    d² – 2cdCos (A – B)

 

                               =

                               =

                               =

                               =

                               =  +

                         

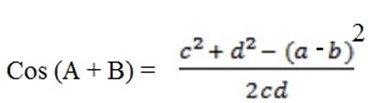
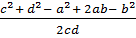
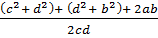
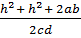
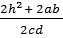
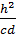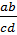
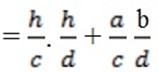
            But,   = Cos A,  = Cos B,  = Sin B

                        Cos (A – B) = Cos A Cos B + Sin A Sin B

Tan (A + B) =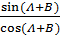

                        =

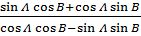
Divide numerator and denominator by Cos A Cos B

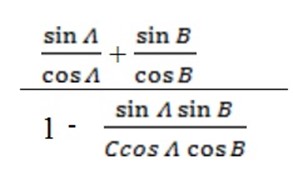
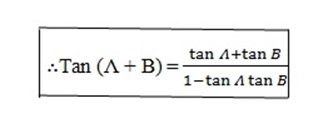
Tan (A – B) =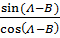

                        =

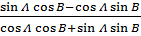
Divide numerator and denominator by Cos A Cos B

            =                                                                                                                                     

            =

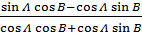
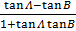
            ∴Tan (A – B) =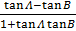

Example 1.9

1. Without using tables, evaluate the following

a) Tan (195^o)

b) Sin 15^o

c) Cos 75^o

d) Tan 15^o

Solution

a) Tan 195^o = tan (135^o + 60^o) =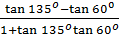

                          

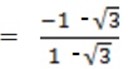
b) Sin 15^o = sin (45^o 30^o) = sin 45^o Cos 30^o – Cos 45^o sin 30^o

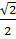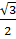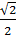                                            =     x  –  x

                                             =    –

                                        

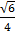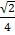
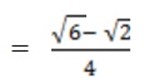
c) Cos 70^o = Cos (45^o + 30^o) = Cos 45^o Cos 30^o – sin 45^o sin 30^o

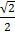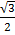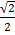            =  x  –  x

            =   –

           

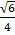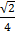
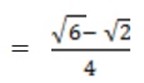
d) Tan 45^o = tan (45^o – 30^o)           

                        =

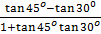
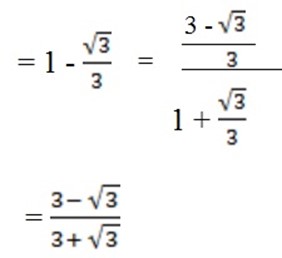
Example 1.10

1. Prove that Cosec θ = Sin θ + Cos θ cot θ

Solution

Take the RHS

            Using cot θ =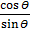

            Cosec θ = sin θ + Cos θ x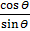

                        =  +

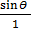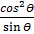
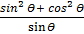                        =  (common denominator)

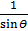                        =  (sin² θ + Cos ²θ)

                        = Cosec θ

            RHS = LHS, hence proved

Solution

Take the RHS
                                                                                          

                   = 

                  = 

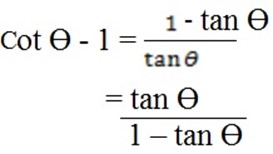
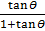
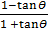
RHS = LHS, hence proved

Exercise 1.11

1.   Simplify a) sin ⁴θ – Cos ⁴ θ

            b)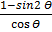

            c) (Sin θ + cos θ) ² – 2sin θ cos θ

            d)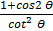

2.  Provide the identities

            a) tan θ cot θ sec θ cos θ = 1

            b)  =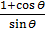

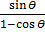
            c)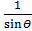 =  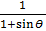 = 2 tan θ sec θ

            d) tan θ + cot θ = Sec θ Cos θ  = 1

            e) (aCos θ  + b sin θ) ² + (-asin θ + bCos θ) ² = a² + b²

            f) (Cosec θ – Cot θ) ² =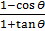

            g)  tan θ + Cot θ = sec θ Cosec θ

            h) (Cos θ – sin θ) ² + (Cosec θ + sin θ) ² = 2

             3.  Compute without tables or calculators

            a) sin 15^o        b) sin 75^o       c) tan 15^o       d) tan 75^o       c) sin 195^o

             4.  Prove the following identities

a) Sin (A +B) + sin (A – B) = 2sin A cos B

            b) Sin (A +B) + sin (A – B) = 2sin A sin B

            c) Cos (A +B) + cos (A – B) = 2cos A cos B

            d) Cos (A +B) + cos (A – B) = 2sin A sin B

5. Simplify the following

            a) Sin (A + 2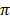r)

            b) Cos (A + )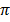

            c) Sin (A + )

            d) Cos (A + 2)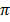

6. Express 6 sin (x + 60^o) in the form of p sin x + Q sin x

            7.   If cos A =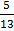, tan B = , A and B being acute. Evaluate the following

            a) Cos (A + B)

            b) Tan (A + B)

            c) Sin (A + B)

Double angle formulae

By applying the knowledge of compound angles, it is clear that

(1). sin 2x = sin (x + x)

                = sinx cosx + cosx sinx

         Thus sin 2x = 2sin x cos x

 (2). Cos 2x = cos x cos x – sin x sin x

                        = cos² x – sin² x

            From cos ² x + sin² x = 1

                        Sin² x = 1 – cos² x

                        Cos² x = cos² x – (1 + cos²x)

                                    = cos² x + cos² x – 1

                         Cos2x =   2cos²x – 1

            But cos² x = 1 – sin² x

                        Cos² x – sin² x = cos 2x

                        1 – Sin2 x – sin² x = cos 2x

                        1 – 2 sin²x = cos²x

                        ∴Cos²x = cos²x – sin² x = 2cos² x – 1 = 1 – 2sin² x

            3.  Tan 2x = tan (x + x)

                        =

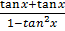
            Tan 2x =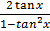

Exercise 1.12

1.   a) Express sin 3x in terms of cos x

      b) Express cos 3x in terms of cos x

      c) Express tan 3x in terms of tan x

2.   Use double angle formulae to prove that

        a) Sin 4x = 8cos³x sin x – 4cos x sin x

         b) Cos 4x = 8cos⁴ x – 8 cos² x + 1

How to write cos 2A and sin 2A in terms of tan A

From double angle formula, it is clear that,

a) Cos 2A =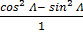

            From cos² A + sin² A = 1

            Cos 2A =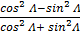

Divide the numerator and denominator by cos ² A we have

 

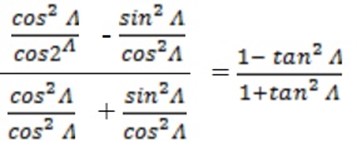
b) Similarly, from double angle formula of sine, we see that

            Sin 2A =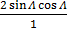

                        =

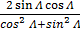
            Dividing numerator and denominator by cos² A, we have

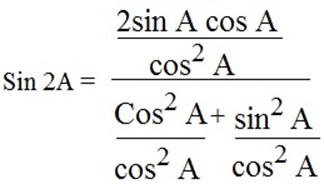
                         Sin 2A =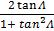

Example 1.13

Solve sin (2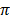 + θ) + cos (θ – ) = 1, where 0^o ≤ θ ≤ 360^o

Solution

Cos 2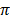 = 1, sin 2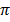= 0, cos  = 0 and sin  = 1

Expand the left part of the equation i.e sin (2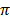 + θ) + cos (θ – )

Sin 2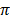cos θ + cos 2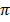sin θ + cos θ cos  + sin θ sin  = 1

Sin θ + sin θ = 1

            2sin θ = 1

            Sin θ =

            θ = 30^o, 150^o

Exercise 1.14

1.   Solve the following trigonometric equations for 0 ≤ θ ≤ 360^o

            a) Sin θ – 1 = 0

            b) 2cos θ =

            c) Tan θ =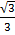

            d) Tan 3θ = 1

            e) 2cos θ

            f) Cos θ = sin θ

            g) Sin θ = 2

2.  Solve for θ, where 0^o ≤ θ ≤ 360^o

            a) cos² θ – 2cos θ = 0

            b) 2sin² θ + sin θ – 1 = 0

            c) 2cos 2 + 3cos θ + 1 = 0

            d) 4sin2 + 4sin θ = 3

3.  Solve for θ, where 0^o ≤ θ ≤ 360^o

            a) cos (sin θ) = 1

            b) cos 2θ + sin θ – 1

            c) 2sin 2θ – tan θ = 0

            d) Sin 4θ cos 2θ cos 4θ sin 2θ =