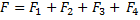Definition
Vectors are any quantity that possess both magnitude and direction .
Example
(i) Displacement
(ii) Velocity
(iii) Acceleration
REPRESENTATION OF A VECTOR
The vector quantity is always described by using two capital letters with respect to arrow on top or small letters with respect to bar at the bottom.
n
A B
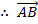or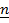 
COMPONENTS OF VECTORS.
This depends on the dimension of vector as follows;
(i) For two dimensions namely as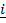 
and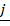 
Where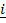 
=x- value
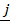= y – value
e.g.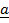 
= (x,y) coordinate form
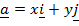component form
Diagram
For three dimensions
Re: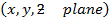 
This involves three components namely as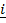 
, 
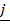and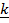 
Where,
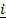= x – value
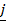= y – value
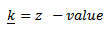
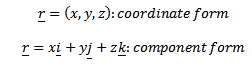
TERMINOLOGIES APPLIED IN VECTOR ANALYSIS
1. PARALLEL VECTORS
These are vectors having the same direction.
e.g
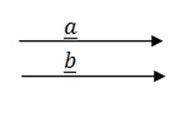
2. EQUAL VECTORS
These are vectors having the same magnitude and direction.
e.g.
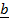= 5N
= 5N
3. NEGATIVE (OPPOSITE) VECTORS
These are vectors having the same magnitude but opposite direction.
Hence
(i)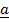 
=-
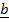(vector in opposite direction
(ii) 
= 
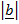= b vector on the same direction
FREE VECTORS
These are vectors which originate from different points.
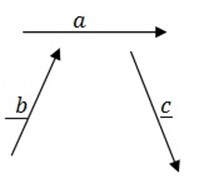
POSITION VECTORS
These are vectors which originate from the same points.
NB:
– Position vector of 
= 
– 
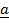
– Position vector of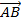 
=
– 
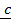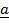
– Position vector of 
= 
– 
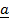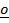
– Position vector of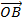 
= 
– 
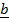NULL VECTORS
These are vectors which have a magnitude of zero ( length of zero) or
These are vectors which contain zero point
Eg.
= (0,0)
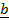= (0,0,0)
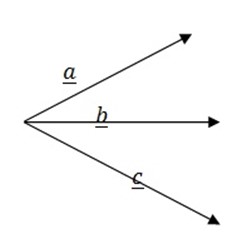
COLLINEAR VECTORS
– These are vectors which lie on the same line.
i.e.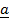 
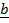
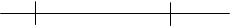
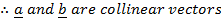
COPLANAR VECTORS
These are vectors which lie on the same plane.
, 
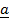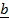and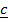 
are coplanar vector
NB:
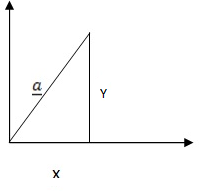
Consider the vector diagram below;
Where
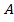= initial (starting) point
B = Final (terminal) point
OPERATION IN VECTORS
These are
(i) Addition
(ii) Subtraction
(iii) Multiplication
i. ADDITION OF VECTORS
Suppose two dimensional vectors
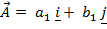
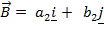
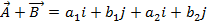
Suppose three dimensional vectors
+ 
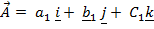
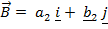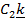
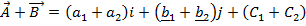k
RESULTANT VECTOR
Is the single vector which represents the effect of all vectors acting at a point.
Consider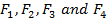 
are acting at a point
Hence
Where F is the result force/ vector