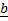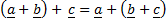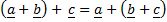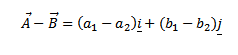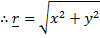LAWS OF VECTORS – ADDITION
A: TRIANGULAR LAW OF VECTORS APPLICATION
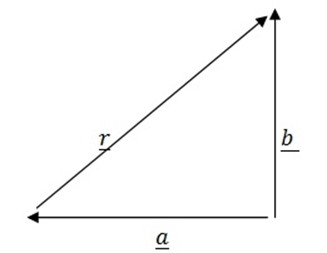
Consider the vector diagram below;
+ 
– 
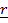= 0
= 
+ 
+ 
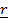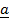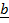
Where r is the resultant vector
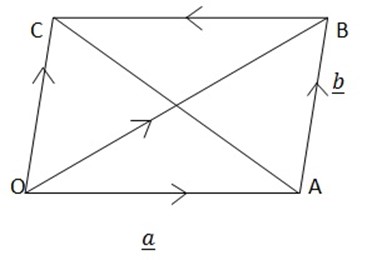
B. PARALLELOGRAM LAW OF VECTORS ADDITION
– Consider the vector diagram below
+ 
= 
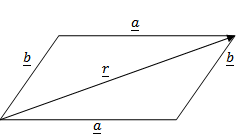
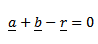
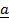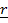…………………………(i)
+ 
– 
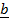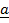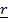= 0
+ 
= 
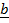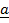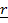……………………………(ii)
From (i) and (ii) above
Proved
(ii) Addition of vectors is associative for any three vectors a, b and c
Proof
Consider the vector diagram below;
Individual but not considered
–
= 
= 
= 
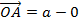
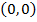
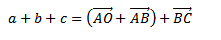
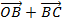
……(i)
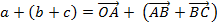
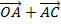
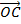…………………..(ii)
From (i) and (ii) above
= 
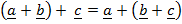
Proved
(iii) For….. of additive identity
For every vector a, we have;
Where;
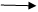0 
The null (zero) vector
(iv) Entrance of addictive reverse
For every vector a we have
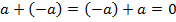
Where
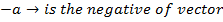
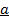→ is the positive of vector
→ is the null vector
ii. SUBTRACTION OF VECTORS
Suppose two dimensional vectors
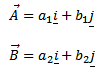
Hence
= 
= 
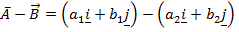
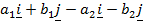
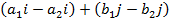
– Suppose three dimensional vectors
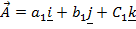
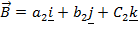
Hence
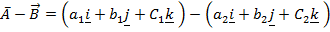
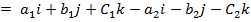
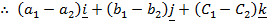
Question 1
1. If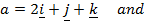 
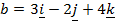
(a Find (i)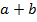 
(ii)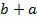 
Comment of the results in (a) above
Question 2
Given that
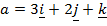
(i) Find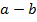 
(ii)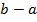 
(b) Comment on the results in a above
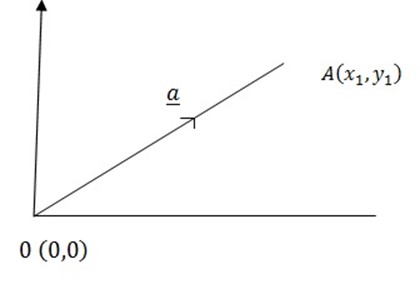
MAGNITUDE OF A VECTOR
– The magnitude of a vector is a measure of length of the vector.
– – This is denoted by the symbol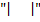 
(a) Consider two dimensional vector
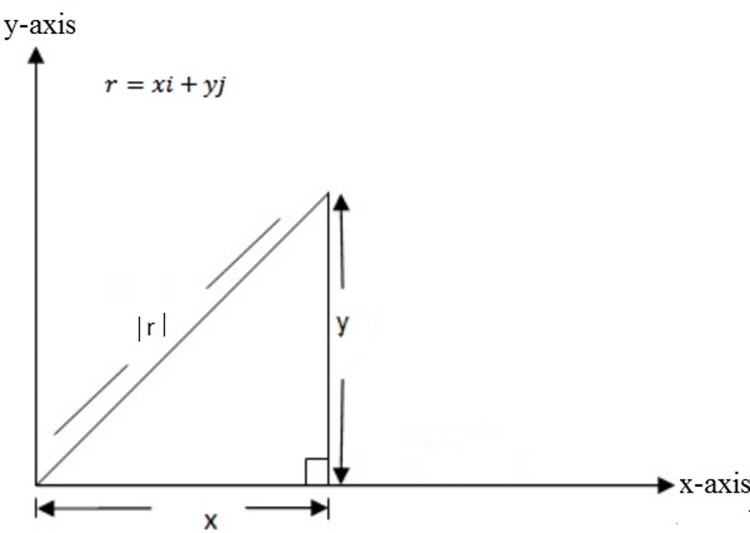
By using Pythagoras theorem
Recall;
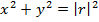
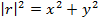
Where
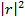– is the magnitude/ module of the vector r
(b) Consider three dimensional vector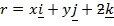 
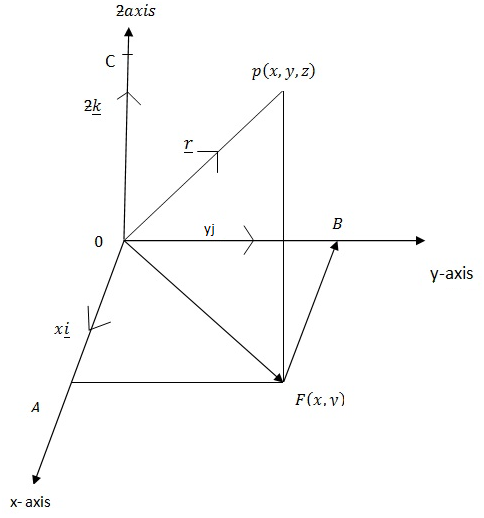
RECTANGULAR RESOLUTION OF A VECTOR
Let: 
be three rectangular axes and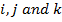 
be three unit vectors parallel to 
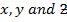axes respectively.
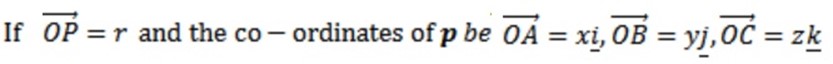
Consider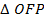 
+
+ 
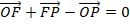
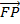
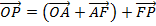
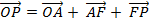
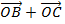
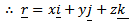
Also consider the right angled OFP
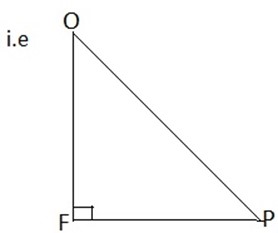
Using Pythagoras theorem
i.e a2 + b2 = c2
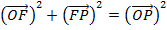
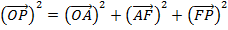
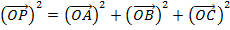
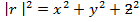
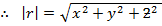
Where
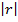= is the magnitude of the vector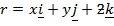 
Question
Given that
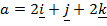
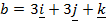
Find 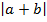
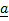