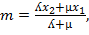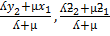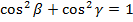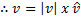DIRECTION RATIO AND DIRECTION COSINES
I. DIRECTION RATIO
Suppose the vector
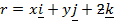
The direction ratio is given by
II. DIRECTION COSINE
Consider the vector
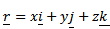
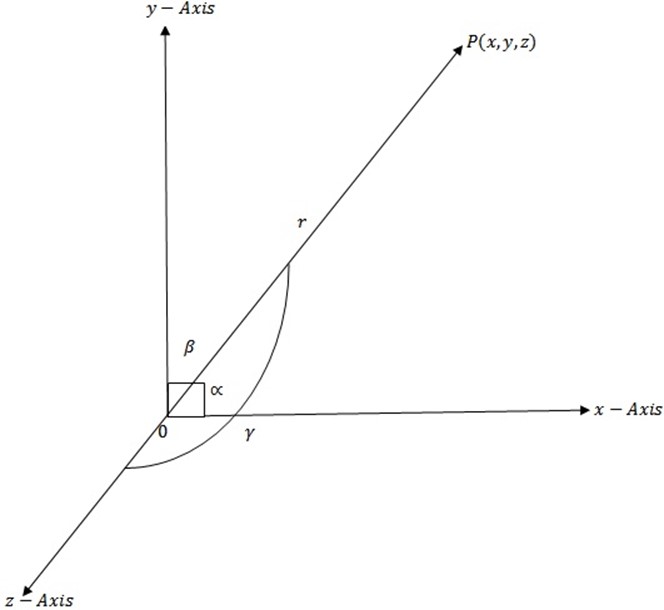
From three dimension plane.
 Makes angles
Makes angles 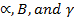 with
with 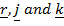 direction respectively
direction respectively
Hence
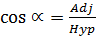
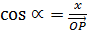
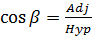

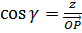
Therefore the direction cosines are
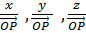
FACT IN DIRECTION COSINES
– Suppose the vector
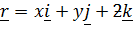

Also the direction cosines are
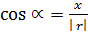
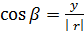
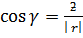
Hence
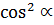 +
+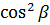 +
+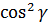 = 1
= 1
– The sum of square of the direction cosines is one.
Proof
i.e 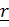 = x
= x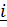 +y
+y +z
+z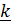
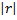 =
=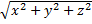
Also
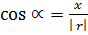

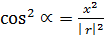 —————-(i)
—————-(i)
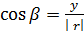
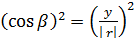
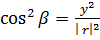 ———————-(ii)
———————-(ii)
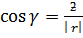
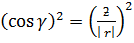
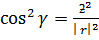 —————————-(iii)
—————————-(iii)
Adding the equation (i) , (ii) and (iii)
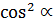 +
+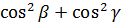 =
=  +
+ 
= 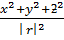
But
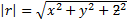
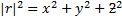
 +
+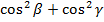 =
=
UNIT VECTOR
-Is the vector whose magnitude (modules) is one line a unit
-The unit vector in the direction of vector a is donated by read as ” a cap” thus
NOTE:
Any vector can be compressed as the product of it’s magnitude and it’s unit vector
i.e
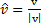
QUESTIONS
1. Find a vector in the direction of vector 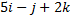 which has a magnitude of 8 units
which has a magnitude of 8 units
2. Find the direction ratio and direction cosines of the vector 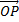 where p is the point (2, 3, -6)
where p is the point (2, 3, -6)
THE FORMULA OF DISTANCE BETWEEN TWO POINTS
Suppose the line joining the points 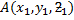 and
and 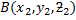 whose position vectors are a and b respectively
whose position vectors are a and b respectively


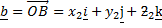
HENCE
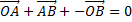
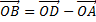
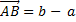
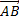 =
=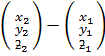
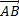 =
=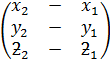
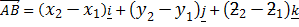
Hence

-Formula distance between two point
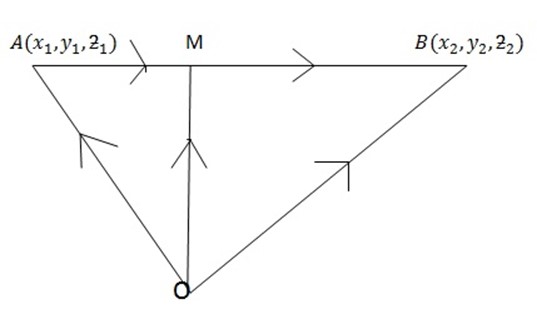
MID POINT OF A LINE
Suppose M is the point which divide the line joining the points  and
and  whose position vectors are respectively a and b into two equal parts
whose position vectors are respectively a and b into two equal parts
i.e
a = 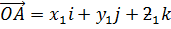
b = 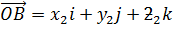
Hence
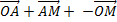
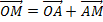


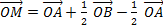
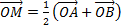


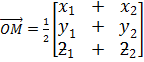
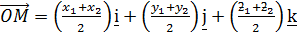
Therefore
The co-ordinate of M is

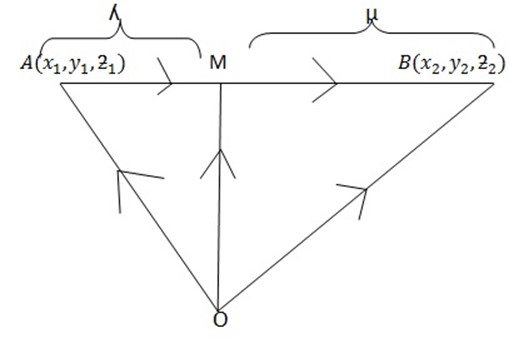
INTERNAL AND EXTERNAL DIVISION OF A LINE (RATIO THEOREM)
I. INTERNAL DIVISION OF A LINE
– Suppose M- is the point which divides the line joining the points 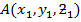 and
and  whose point vectors are a and b respectively internally in the ratio X:ee
whose point vectors are a and b respectively internally in the ratio X:ee
a = 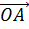 =
=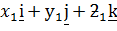
b = 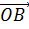 =
=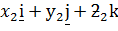
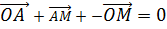

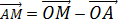 ……………(i)
……………(i)
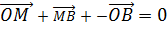
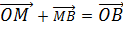
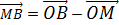 ……………(ii)
……………(ii)
By using ratio theorem
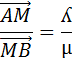
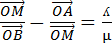
By using multiplication
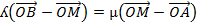
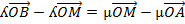
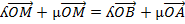



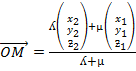
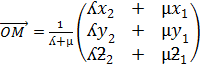
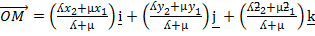
The ordinate form of M is