II. EXTERNAL DIVISION OF A LINE
Suppose M- is the point which divides the line joining the points 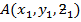 and
and 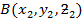 where position vectors are
where position vectors are 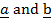 respectively , externally is the ration
respectively , externally is the ration 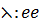
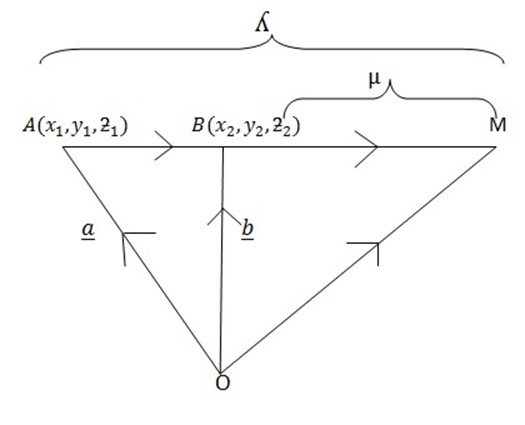
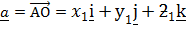
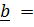
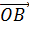 =
=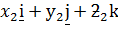
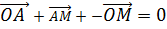
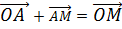
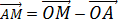 ……………(i)
……………(i)
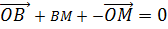
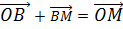
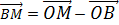 ……………(ii)
……………(ii)
By using ratio theorem
i.e
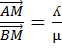
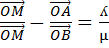
BY CROSSING MULTIPLICATION
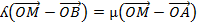
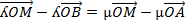
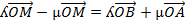
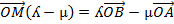
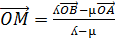
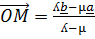
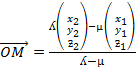
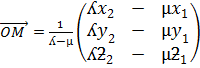
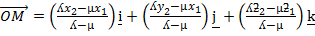
Therefore
The co-ordinate of M
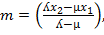
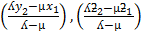
External division of a line where 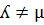
QUESTIONS
1.Find the length of the line 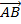 of
of 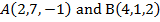
2. Find the position vector which divides line 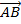 having point
having point 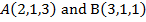 into two equal points.
into two equal points.
3. A and B are two points whose vectors are 3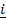 +
+ 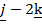 and
and 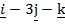 respectively. Find the position vector of the points dividing AB.
respectively. Find the position vector of the points dividing AB.
(a) Internally in the ratio 1:3
(b) Externally in the ratio 3:1
III. MULTIPLICATION OF A VECTOR
(A) SCALAR MULTIPLICATION OF A VECTOR
In this case a vector is multiplied by a certain constant called scalar
Let
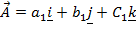
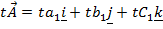
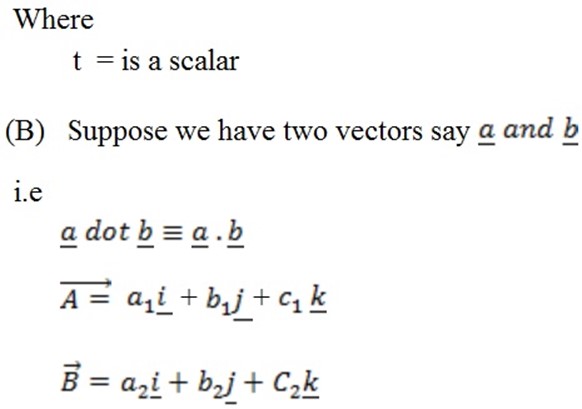
THEREFORE
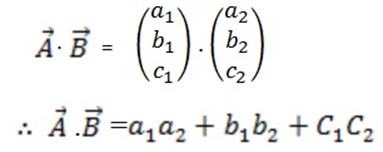
QUESTIONS
If 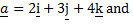
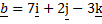
(a) Find (i) 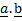
(ii)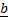 .
.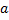
(b) Comment on results in 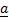 above
above
DEFINITION OF DOT PRODUCT
For vectors 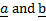
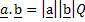
Where
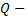 is the above between
is the above between 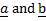
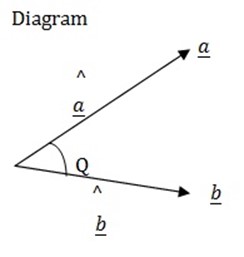
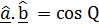
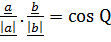
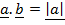
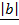 cos Q
cos Q
CHARACTERISTICS
1. 1. PARALLEL VECTOR
Two vector are said to be parallel of the angle between them is zero
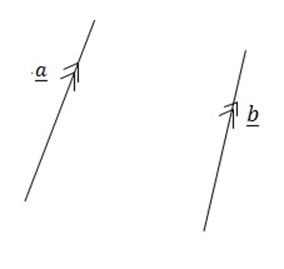
Mathematically
From
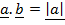
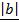 = cos Q
= cos Q
But Q = 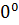
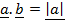
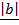 = cos Q
= cos Q
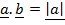
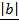
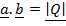
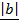
This is one among the
2. 2. Orthogonal vectors
Two vectors are said to be orthogonal of the angle between them is 90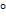
Mathematically
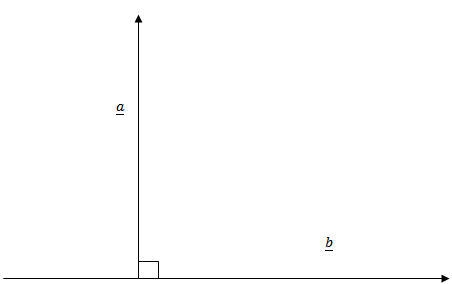
From
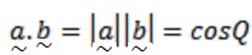
But Q = 90 (orthogonal or perpendicular vector)
(orthogonal or perpendicular vector)
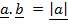
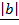 = cos 90
= cos 90
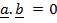
This is conditional for the orthogonal vector
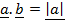
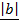 cos Q
cos Q