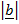 2 =
2 = 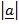 2 +
2 + 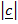 2 – 2
2 – 2 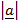
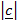 cos
cos 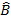
Therefore
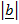 2 =
2 = 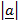 2 +
2 +  2 – 2
2 – 2 
 cos
cos 
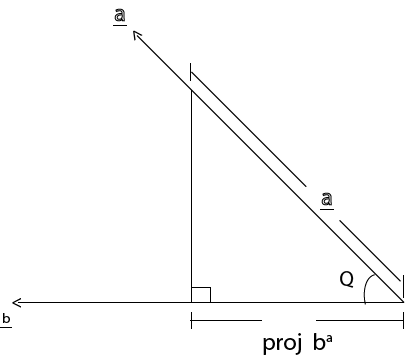
02. USED TO FIND THE PROJECTION OF ONE VECTOR ONTO ANOTHER VECTOR
– Suppose the projection of a onto b
i.e
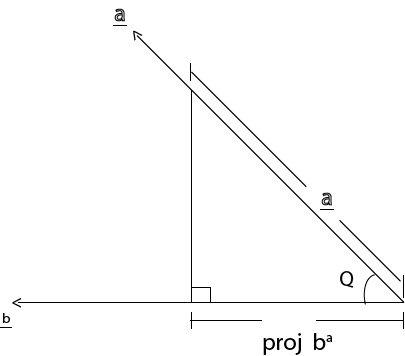
Cos Q = 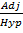
Cos Q = 
proj 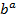 =
= 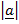 cos Q ———– i
cos Q ———– i
Also
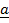 .
. 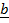 =
= 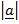
 cos Q
cos Q
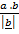 =
= 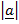 cos Q ———–ii
cos Q ———–ii
Equalizing i and ii as follows;
proj 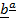 =
= 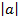 cos Q =
cos Q = 
proj 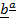 =
= 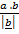
similary
proj 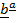 =
= 
Where;
Proj 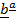 = projection of
= projection of 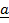 onto
onto 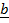
Proj 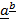 = projection of
= projection of 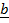 onto
onto 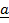
VECTOR PROJECTION
This is given by
V proj =
= .
. 
And
V. proj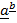 =
=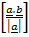 .
. 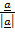
Where;
V. proj  = vector projection of
= vector projection of 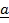 onto
onto 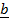
V. proj  = vector projection of
= vector projection of  onto
onto 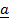
03. TO FIND THE WORKDONE
– Consider the diagram below

Force applied (F) = component of tone
cos Q = 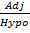
Cos Q = 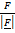
F = 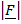 Cos Q
Cos Q
Also
Distance d = 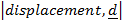
d = 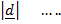 ….ii
….ii
Hence
Work done = Force applied (F) x distance (d)
W.D = F x d
W. D = 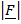 cos Q x
cos Q x 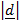
= 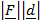 cos Q
cos Q
= 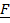 .
. 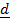
W.D = 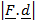
Note
i) Force F in the direction of vector 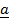
Force applied = F.
ii) Distance in the direction of vector 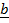
Displacement 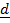 = d.
= d.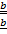
Individual
i) 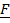 = 2i +
= 2i + 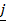 + 2
+ 2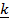
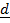 = i +
= i + 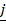 +
+ 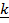
W.D = 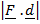
04. TO PROVE COMPOUND ANGLE FORMULA OF COSINE
i.e cos (A + B) = cos A cos B – sin A sin B
 – consider the vector diagram below.
– consider the vector diagram below.
Diagram

 = (cos A)
= (cos A) 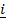 + (sin A)
+ (sin A) 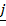
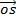 = (cos B)
= (cos B) 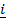 – (sin B)
– (sin B) 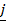
Hence
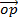
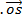 =
= 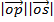 cos (A + B)
cos (A + B)
but
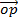 .
. 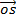 =
= 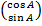
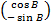
= cos A cos B + -sin A sin 0
= cos A cos B – sin A sin B
Also
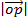 =
= 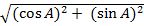
= 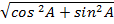
= 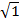
= 1
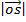 =
= 
= 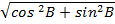
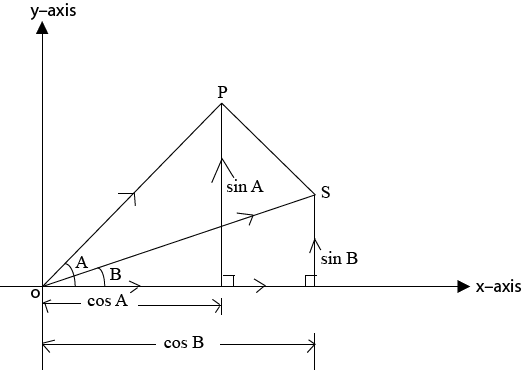
= 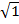
= 1
Therefore
Cos A cos B – sin A sin B = (1)(1) cos (A + B)
Cos (A + B) = cos A cos B – sin A sin B
Proved
Pg. 2 drawing
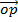 = (cos A)
= (cos A) 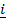 + (sin A) j
+ (sin A) j
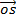 = (cos B) I + (sin B)
= (cos B) I + (sin B) 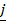
Hence
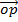 .
.  =
= 
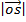 cos (A – B)
cos (A – B)
But
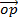 .
. 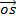 =
= 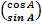
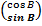
 .
. 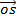 = cos A cos B + sin A sin B
= cos A cos B + sin A sin B
Also
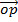 =
= 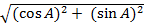
= 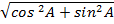
= 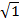
= 1
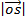 =
= 
= 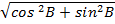
= 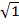
= 1
There
Cos A cos B + sin A sin B = (1) (1) cos (A – B)
Cos (A – B) = cos A cos B + sin A sin B
Proved