06. TO PROVE THAT AN INSCRIBED ANGLE SUBTENDING A SEMI – CIRCLE IS A RIGHT ANGLE
– Consider the vector diagram below.
Pg. 2 drawing
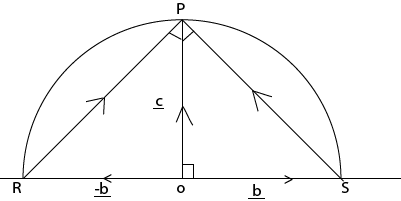
To prove that
< S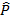 R = 900
R = 900
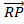 .
.  = 0
= 0
-b +  + –
+ –  = 0
= 0
– 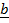 +
+ 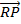 =
= 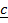
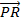 =
= 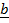 +
+ 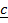
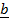 +
+  + –
+ –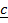 = 0
= 0
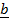 +
+ 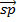 =
= 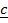
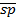 =
= 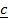 –
– 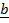
Hence
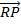 .
.  = (
= (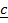 +
+ 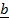 ) (
) (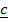 –
– 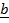 )
)
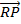 .
. 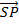 =
= 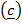 2 – (
2 – ( 2
2
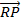 .
. 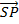 =
= 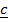 2 –
2 –  2
2
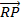 .
. 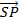 =
= 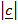 2 –
2 – 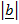 2
2
But
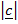 =
= 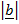 = radius, r
= radius, r
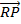 .
. 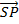 = 0
= 0
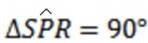
Proved
QUESTION
17. Find the projection of 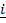 + 2
+ 2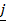 – 3
– 3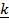 onto
onto 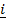 + 2
+ 2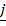 + 2
+ 2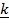
18. Find the vector projection of 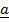 onto
onto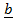 . If
. If 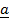 = 2
= 2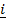 +2
+2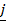 +
+  and
and 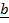 = 3
= 3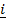 +
+ 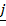 + 2
+ 2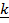
19. Find the work done of the force of (2i + 3i + k) n s pulling a load (3i + j k) m
20. Find the work done of the force of (2i + 3j + k) N is pulling a load a distance of 2m in the direction of 2m in the direction of
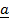 = 3
= 3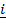 + 2
+ 2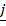 + 2
+ 2
21. Find a vector which has magnitude of 14 in the direction of 2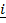 + 3
+ 3 +
+ 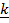
CROSS (VECTOR) PRODUCT (X or 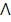 )
)
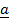 x
x 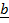 =
=  sin Ø.
sin Ø. 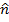
Where
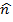 – is the unit vector perpendicular to both vector
– is the unit vector perpendicular to both vector 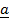 and
and 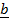
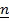 =
= 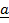 x
x 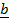
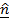 =
= 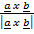
Hence
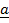 x
x 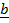 =
= 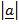
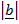 sin Ø.
sin Ø. 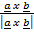
1 = 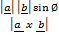
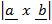 =
= 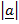
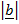 sin Ø
sin Ø
Therefore
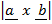 =
= 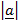
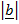 sin Ø
sin Ø
OR
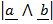 =
= 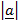
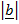 sin Ø
sin Ø
Where
Ø – is the angle between the vector 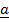 and
and 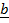
Again
Suppose the vector
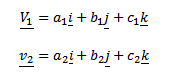
Hence
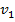 +
+ 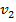 =
= 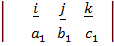
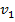 +
+ 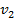 =
= 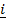
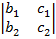 – j
– j 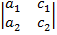 +
+ 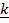
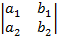
Note
i) If you cross two vectors, the product is also the vector.
ii) Cross (vector) product uses the knowledge of determinant of 3 x 3 matrix.
iii) From the definition.
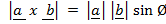
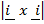 =
= 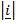
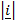 sin
sin 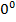
Individual
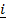 = (1, 0, 0)
= (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
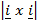 = (1) (1) (0)
= (1) (1) (0)
 = 0
= 0
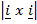 = 0
= 0
Hence
i x i = j x 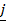 =
=  x
x 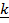 = 0
= 0
iv) From the definition
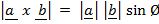
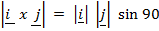
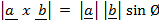

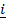 x
x 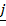 = k
= k
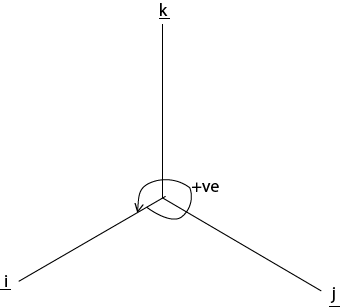
Generally
Consider the component vector
For anticlockwise (+ve)
Pg. 4 drawing
i)  x
x  =
= 
ii)  x
x 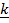 =
= 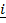
iii) 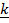 x
x 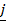 =
= 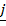
For clockwise (-ve)

i)  x
x  =
= 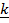
ii) 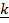 x
x 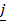 = –
= – 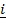
iii) 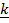 x
x 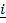 = –
= – 
THEOREM
From the definition
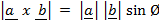
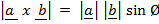
– 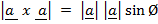
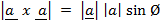
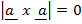
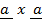 = 0
= 0
Is the condition for collinear (parallel) vectors
a) 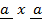 ≠
≠ 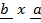
= – 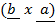
Questions
22. If 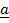 = 2
= 2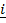 + 6
+ 6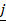 + 3
+ 3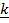 and
and 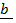 =
= 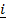 + 2
+ 2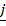 + 2
+ 2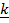 . Find the angle between
. Find the angle between 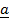 and
and 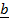
23. Determine a unit vector perpendicular to 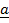 = 2
= 2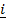 – 6
– 6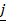 – 3
– 3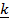 and
and 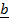 = 4
= 4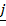 + 3
+ 3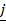 –
– 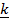
24. If 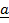 = 2
= 2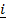 + j + 2k and
+ j + 2k and 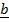 = 3
= 3 + 2
+ 2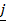 +
+ 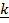
Find 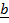 â‹€
â‹€
Box product
-This involves both cross and dot product
Suppose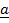 .
. 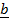 x
x 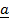 then start with cross (x) followed by DOT (.)
then start with cross (x) followed by DOT (.)
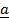 .
.  x
x 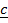 =
=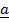 .
. 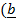 x
x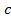 )
)
-This is sometimes called scalar triple product
Note
-If scalar triple product (box product) of three vectors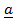 .
.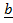 and
and 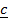 = 0
= 0
-Then the vector 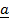 ,
, 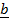 and
and 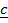 are said to be COMPLANAR
are said to be COMPLANAR
Question
25. If 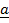 = 2
= 2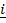 +
+ 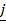 + 2
+ 2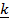
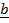 = 2
= 2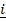 +
+ 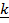 and
and
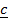 = 3
= 3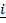 + 2
+ 2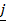 + k
+ k
Find
a) 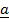 .
. 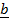 x c
x c
b) 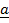 x
x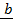 .
. 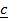
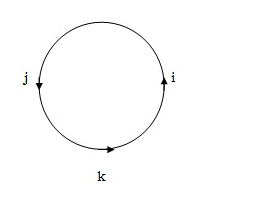
APPLICATION OF CROSS PRODUCT
USED TO PROVE SINE RULE
– Consider the diagram below
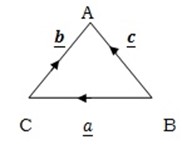
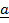 +
+ 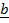 + –
+ – 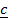 = 0
= 0
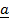 +
+  =
= 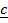
Cross by 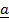 on both sides of
on both sides of
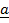 x
x 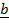 +
+ 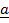 x
x 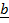 =
= 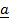 x
x 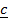
0 + 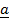 x
x 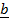 =
= 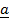 x
x 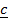
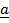 x
x  +
+ 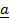 x
x 
Crossing by 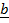 on both sides of eqn …. 1 above
on both sides of eqn …. 1 above
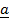 +
+ 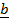 =
= 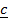
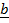 x
x 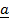 +
+ 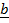 +
+ 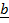 =
=  x
x 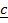
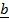 x
x 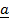 +
+  =
= 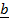 x
x 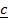
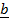 x
x 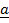 =
= 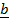 x c
x c
– (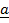 x
x  =
= 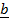 x
x 
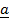 x
x 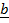 = –
= – 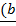 x
x 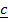 )
)
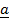 x
x  =
= 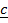 x
x 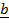
Equation i and ii as follows
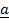 x
x  =
=  x
x 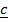 =
=  x
x 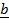
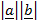 Sin
Sin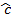 .
.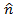 =
=  sin
sin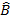 .
.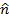 =
= 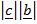 sin
sin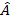 .
.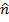
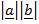 Sin
Sin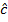 =
= 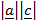 Sin
Sin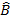 =
=  sin
sin 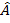
Dividing the whole eqn by
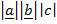
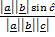 =
= 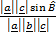 =
=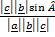
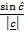 =
= 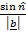 =
= 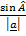
Sine rule