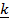USED TO PROVED COMPOUND ANGLE FORMULA OF SINE
Sin (A + B) = sin A cos B + sin B cos A
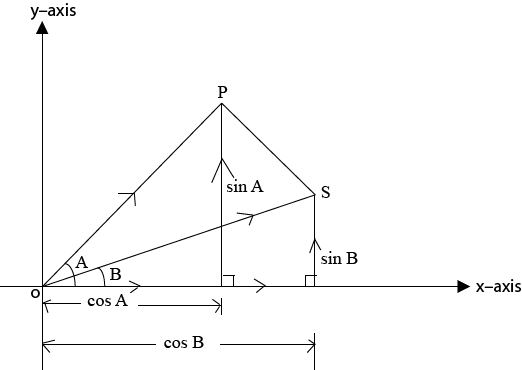
Consider the vector diagram below
Pg. drawing
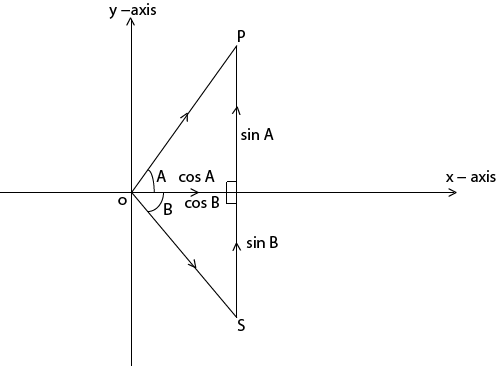
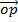 = (cos A)
= (cos A) 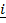 + (sin A)
+ (sin A)  + o
+ o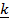
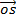 = (cos A)
= (cos A) 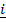 + (sin A)
+ (sin A) 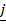 + o
+ o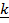
Hence
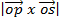 =
= 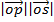 sin (A + B)
sin (A + B)
But
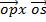 =
= 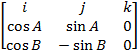
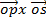 = i
= i 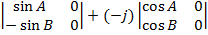 + k
+ k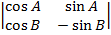
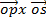 = i (o) – j (o) + k (-cos A sin B – sin A cos B)
= i (o) – j (o) + k (-cos A sin B – sin A cos B)
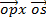 = -k [sin A cos B + cos A sin B]
= -k [sin A cos B + cos A sin B]
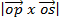 =
= 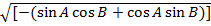 2
2
=  2
2
 = sin A cos B + cos A sin B
= sin A cos B + cos A sin B
Also
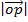 =
= 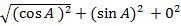
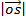 =
= 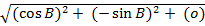 2
2
 2 =
2 =  2 B
2 B
= 1
Therefore
Sin A cos B + cos A sin B = (1) (1) sin (A+B)
Sin (A + B) = Sin A cos B + cos A sin B
Proved
USED TO DETERMINE/ TO PROVE COMPOUND AND FORMULA OF SINE
Sin (A – B) = sin A cos B – Cos A sin B
– Consider the vector diagram below
Pg.6 drawing
 = (cos A)
= (cos A)  + (sin A)
+ (sin A) 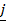 + o
+ o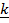
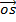 = (cos B)
= (cos B) 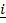 + (sin B)
+ (sin B) 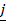 + o
+ o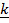
= 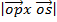 =
=  sin (A – B)
sin (A – B)
but
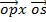 =
= 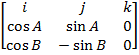
= i 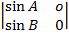 – j
– j 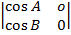 + k
+ k 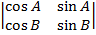
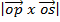 =
= 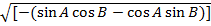 2
2
= 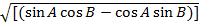 2
2
= sin A cos B – cos A sin B
Also
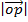 =
= 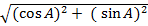 + 0
+ 0
= 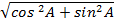
= 
= 1
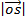 =
= 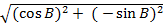
= 
= 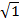
= 1
Therefore
Sin A cos B – cosA sin B = (1) (1) sin (A – B)
Sin (A – B) = sin A cos B – cos A sin B
Proved
USED TO FIND THE AREA OF THE TRIANGLE
– Consider the triangle ABC below
Pg. 7 drawing
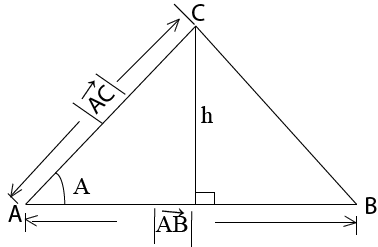
Area (A) = ½ x base (b) x height (h)
A = ½ bh ……i
Also
Sin 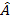 =
= 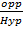
Sin  =
= 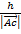
h = 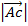 Sin
Sin  ….ii
….ii
And
b = 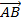 …iii
…iii
Substitute …ii and …iii into 1 as follows
A = ½ 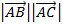 sin
sin 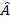
A = ½ 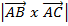
USED TO FIND THE AREA OF PARALLELOGRAM
– Consider the parallelogram below
Pg. 7 drawing
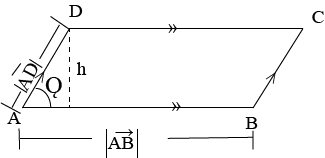
Area = length (l) x height (h)
= A = Lh …i
L = 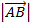 …ii
…ii
Also
Sin Q = 
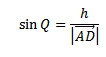
h = 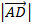 Sin Q….ii
Sin Q….ii
Substitute ii and iii into —1 as follows
Area (A) = 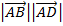 sin Q
sin Q
A = 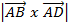
Generally
Area (A) = 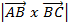
= 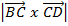
= 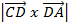
= 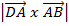
Where
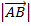 =
= 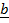 –
– 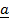
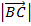 =
= 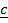 –
– 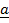
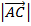 =
= 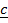 –
– 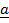
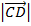 =
= 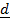 –
– 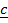
USED TO FIND THE VOLUME OF PARALLELOPIPED
– Consider the diagram below
Pg. 7 drawing
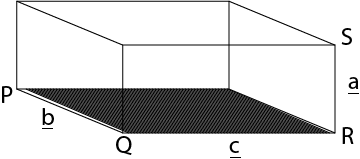
– Suppose P Q R and S are the vertices of the parallelepiped, hence the volume (v) of the parallelepiped is given by:
Volume (v) = base area (A) x height (h)
V =  x
x 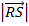
V = 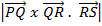
V = 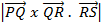
V = 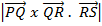
Again, for the sides with position vectors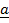 ,
, 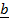 and
and 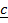
Volume (v) = 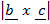 x
x 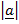
= 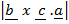
= 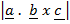
USED TO FIND THE VOLUME OF A TETRAHEDRON
– Consider the tetrahedron with vertices P, Q, R and S
Pg. 8 drawing

Volume (v) = 1/3 x base area x altitude
V = 1/3 x ½ 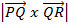 x
x 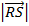
V = 1/6  x
x 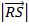
V = 
Therefore
Volume = 1/6 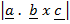
USED
TO FIND THE VECTOR PERPENDICULAR TO THE PLANE
– Consider the diagram below
Pg. 8 drawing
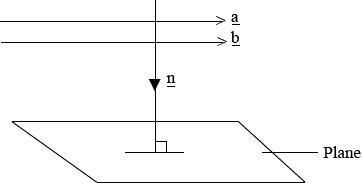
Where
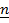 = is the vector perpendicular or normal to the plane
= is the vector perpendicular or normal to the plane
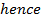
 =
=  x
x 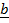
Question
26. Find the area of the triangle ABC whose vertices are A (2, 1, 1) B (3, 2, 1) and C (-2, -4, -1)
27. The position vector of the points A, B and C are (2, 4, 3), (6, 3, -4) and (7, 5, -5) respectively. Find the angle between 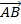 and
and 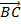 and hence the area of the triangle ABC
and hence the area of the triangle ABC
28. Find the area of the parallelogram whose vertices P, Q and R are (2, 1, 1), (3, 2, 1) (2, 4, 1)
29. Find the volume of the parallelepiped the edges are A (1, 0, 2) B (2, -1, 3) C (4, 1, 3) and D (1, -1, 1)
30. Find the volume of the tetrahedron whose sides are 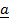 = 2
= 2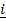 +
+  ,
, 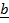 =
= 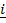 – 3
– 3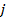 ` +
` + 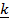 , and
, and 
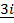 –
– 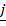 + 2
+ 2