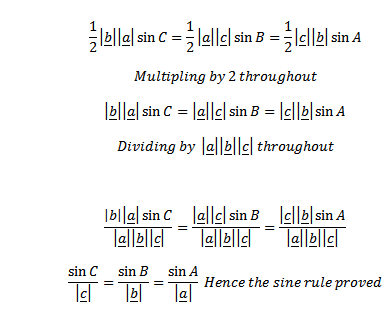COLLINEAR AND COPLANAR VECTORS
1. COLLINEAR VECTOR
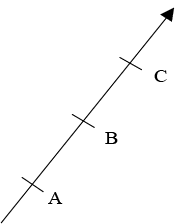
These are vectors having the same slope (re direction).
Pg. 10 drawing
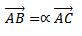
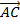 = μ
= μ 
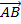 = t
= t 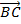
Where
Æ›, μ and t are scalar
Again 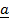 and
and 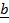 to be collinear
to be collinear  x
x 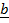 = 0
= 0
2. COPLANAR VECTOR
These are vectors which lie on the same plane
Eg. Pg. 10 drawing

For the vectors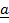 ,
, 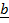 and
and 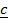 to be coplanar
to be coplanar
 = 0
= 0
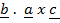 = 0
= 0
 = 0
= 0
Generally
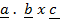 =
= 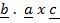 =
= 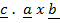 = 0
= 0
Question
31. Given that
 = 3
= 3 + 4
+ 4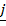

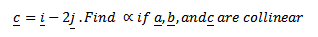
32. Find the value are collinear vectors 2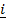 –
– 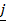 +
+ 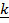 ,
, 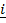 + 2
+ 2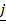 + 3
+ 3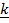 and 3
and 3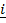 +
+ 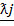 + 5
+ 5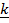 are coplanar.
are coplanar.
33. Find unit vector in the direction of 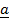 = 6
= 6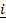 + 3
+ 3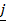 +
+ 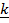 and state its length
and state its length
LINEAR COMBINATION OF VECTORS
Suppose that 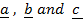 are vectors and
are vectors and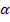 , β and γ are real numbers (sealers). Then a vector
, β and γ are real numbers (sealers). Then a vector 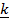 =
= 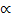
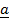 + β
+ β 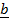 + γ
+ γ 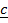 is a linear combination of vectors
is a linear combination of vectors 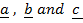
NB
To solve vectors means to put the vectors into linear form
Question
34. If 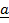 =
= 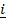 +
+ 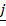 ,
, 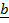 =
= 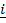 –
– 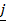 and
and 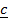 = 3
= 3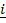 – 4
– 4 resolve
resolve 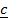 into vectors parallel to
into vectors parallel to 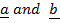
35. Express the vector r = 10 – 3
– 3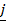 –
– 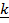 as a linear function of
as a linear function of 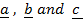 given that
given that
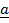 = 2
= 2 –
–  +
+ 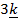
 = 3
= 3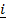 + 2
+ 2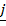 –
–  and
and
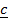 = –
= –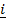 + 3
+ 3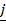 – 2
– 2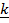
Note: Required to be placed in a right position
Subtopic: Dot Product
Proving cosine rule using dot product
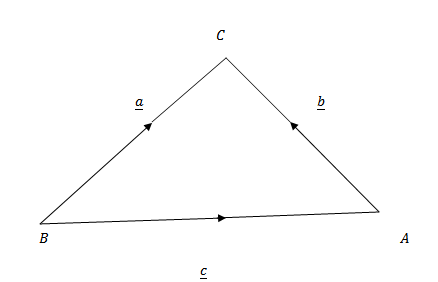
Consider the triangle ABC above
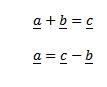
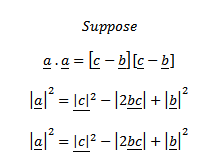
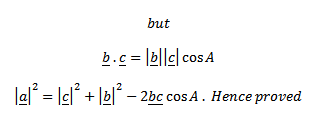
Subtopic: Cross Product
Proof of sine rule Consider the ∆ABC with sides A,B and C respectively
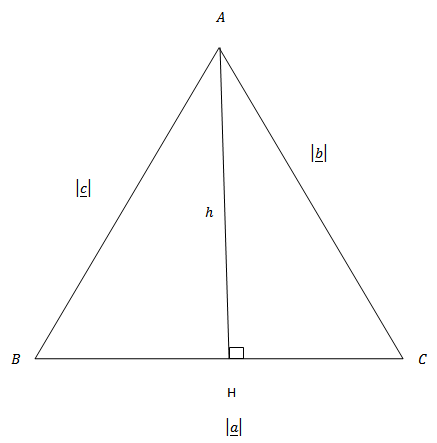
Construct a line AH which lies on BC and perpendicular.
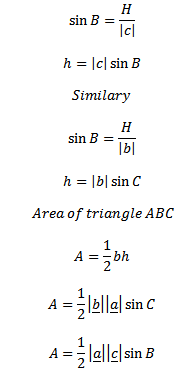

Equating area