Form 3 Mathematics – RATES AND VARIATIONS

RATES:-

When sets or quantities of different kinds are related, we use the word rate.

i.e 1. A rate of pay of 10,000/= Tsh per hour (money– time)

2. The price of juice is 700/= Tsh per litre (money –weight of juice)

3. The average speed of 80 kilometres per hour (distance- time)

Therefore the rate is the constant relation between two sizes of two quantities concerned.

NOTE:

Rates deals with the comparison of two quantities of different kinds.

Example

1. Hiring a car at a charged rate of Tsh 2,000/= per kilometer.

(a) A journey of 40 kilometers will cost 40 x Tsh 2,000= Tsh 80,000/=

(b) A journey of 100 kilometres, costs 100 x Tsh. 2,000= Tsh.200,000/=

If we state the rate we always give two quantities concerned and the unit measurement.

E.g: Average speed is written as 100 kilometres per 2 hours or 50 kilometres per one hour.

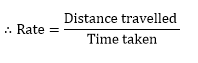
Rates can also written in a ratios form.

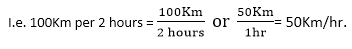
Rate of Exchange

People in any country expect to pay and be paid in currency of their own country. It is necessary to exchange the currency of the first country for that of the second, when money is moved from one country to another.

i.e: The rate of exchange linked together various currencies of the world, which enable transfer of money and payment for goods to take place between countries.

Consider table below shows the exchange rates as supplied by the CRDB bank effective on May 17, 2007.

Examples

1.    1.  A tourist from Sweden wishes to exchange 1,000 Kronors into Tanzanian shillings. How much does she receive?

Soln.

From the table above

1kron =Tsh. 186.42

1,000Kronor= ?

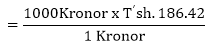
=T shs. 186420

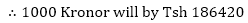
The tourist will receive Tsh. 186420

2.   2.   How much 20,600 Tanzania shillings worth in Indian Rupees?

Soln.

1 Rupee = Tsh. 31.105

? = Tsh. 20,600

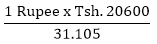
= 662.273 Rupees

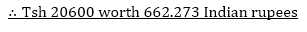
Variations

Direct Variation

The two variables x and y are said to vary directly of the ratio is constant.

The real number K is called the constant of variation.

And relationship may be written as 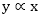which reads as “y is proportional to x“

If y varies directly as the square of x, then 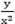=Constant.

And can be written as 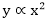and the algebraic relation is y=kx²

When having pairs of different corresponding values of x and y, this equation hold true.

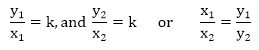
Therefore, we say that x and y vary directly if the ratios of the values of y to the values of x are proportional.

NOTE:

If x and y represent variables such that, then y=kx,

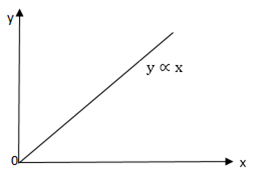
The form of this equation y=kx is similar to y=mx. The graph of y=mx is a straight line passing through the origin, M being the gradient same to the equation y=kx,

The graph is a straight line passing through the origin and gradient is k.

A sketch is like

Examples

If x varies directly as the square of y, and x=4 where y=2, find the value of x when y=8.

Solution

Let x₁= 4 , y₁ = 2, y₂ = 8, x_{2 is required}

But

Inverse variation

 

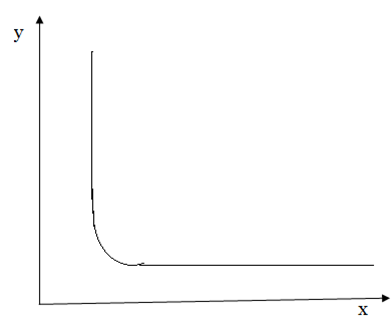
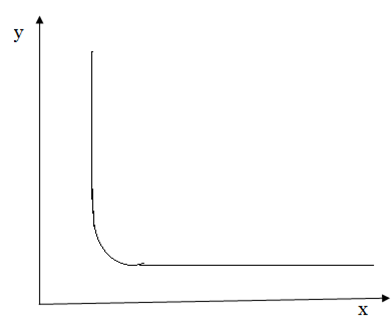
NOTE: The graph does not touch the axis because division by 0 (zero) is impossible.

Example 1

If x varies inversely as y, and x=2, when y=3

Find the value of y when x=18.

Solution.

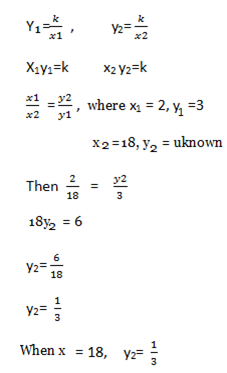
Example 2

 3 tailors are sewing 15 clothes in 5 days. How long would it take for 5 tailors to sew 20 clothes?

Solution

–  Let t = tailors, d = days c= clothes.
A number of tailors is inversely proportional to the number of days.

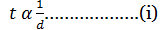
–  The number of tailors in directly proportional to the number of clothes.

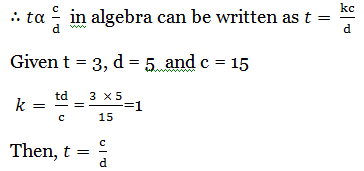
When t = 5, c= 20, d can be found as

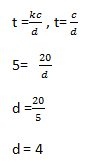
 It takes 4days for to tailors to sew 20 clothes

JOINT VARIATION
If a quantity is equal to a constant times the product of  the two other quantities, then we say that the first quantify varies jointly as the other two quantities.
If x = k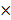 y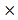z where k is a fixed real number then x varies jointly as y and z.
Similarly if x₁
y₁ z₁ and x₂ y₂ z₂ are corresponding values of the variables x, y and z, then x₁ = k  × (y₁
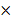z₁) and x₂ = k × (y₂ × z₂)

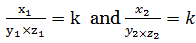
From these we get

 

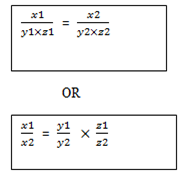
Examples 1

1.      If x varies directly as y and inversely proportional as z and x = 8, when y= 12 and z = 6. Find the value of x when y = 16 and z =4

Solution

Example 2

9 workers working 8 hours a day to complete a piece of work in 52 days. How long will it takes 13 workers to complete the same job by working 6 hours a day.

Solution

Let w= workers

h=hours

d=days

It is a joint variation problem and can be written as