PREDICTION OF DIRECTION AND EXTENT OF CHEMICAL EQUILIBRIUM
At each point in the progress of a reaction, it is possible to formulate the ratio of concentration having the same form as the equilibrium
constant expression .This generalized ratio is called reaction quotient (Q).
For the reaction; 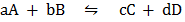 then:-
then:-
QC = 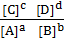
Q p = 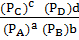
QC differs from KC in that the concentration in the expression is not necessarily the equilibrium concentration.
When the values of KC and QC are compared, one can predict the direction of the chemical reaction.
If Q c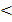 K c the system is not at equilibrium, the reactants must further be converted to products to achieve equilibrium therefore net reaction proceeds from left to right.
K c the system is not at equilibrium, the reactants must further be converted to products to achieve equilibrium therefore net reaction proceeds from left to right.
If Q c = K c the system is at equilibrium
If Q c > K c the system is not an equilibrium, the products must converted to reactants to achieve equilibrium therefore a net reaction proceeds from right to left.
Example:
1.Consider the reaction
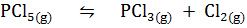
At 2500C, K c = 4.0 x 10-2. If the concentration of Cl2 and PCl3 are both 0.30 M while that of PCl5 is 3.0M, is the system at equilibrium? If not, in which direction does the reaction proceed?
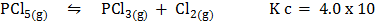 -2
-2
Q c = 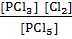
= 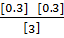
Q c = 0.03 QC ≠ K c, Q c< K c
 The system is not at equilibrium and the reaction proceeds from left to right
The system is not at equilibrium and the reaction proceeds from left to right
2. At 200k, the K p for the formation of NO is 4 x 10-4
N2 (g) + O2 (g) 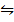 2NO (g)
2NO (g)
If at 200k the partial pressure of N2 is 0.5 atm and that of 02 is 0.25 atm, that of NO is 4.2 x 10-3 atm, decide whether the system is at equilibrium, if not in which direction does the reaction proceed.
K p = 4.0 x 10-4
Q p = 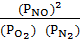
= 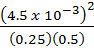
Q p = 1.4112 x 10-4 K p ≠Q p, K p > Q p
 The system is not at equilibrium, therefore the reaction proceeds from left to right
The system is not at equilibrium, therefore the reaction proceeds from left to right
EQUILIBRIUM CONSTANT WITH DEGREE OF DISSOCIATION (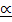 )
)
-It gives to what extent the reactants are converted to products by dissociation.
-This has to be treated similar to moles.
Example1. 0.01 moles of PCl5was placed in 1L vessel at 210K.It was found to be 52.6% dissociated into PCl3 and Cl2. Calculate the K c at that temperature.
PCl5 (g) 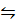 PCl3 (g) + Cl2 (g)
PCl3 (g) + Cl2 (g)
At start: 0.01 0 0
At equilibrium: 0.01-(5.26 x10-3) 5.26 x 10-3 5.26×10-3
=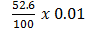
= 5.26 x 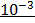
PCl5 = 4.74 x 10-3 moles
PCl3 = 5.26 x 10-3 moles
Cl2 = 5.26 x 10-3 moles
K C = 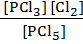
= 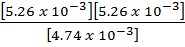
K C = 5.837 x 10-3 moles
2. At 1 atm and 85oC, N2O4 is 50% dissociated, Calculate the equilibrium constant in terms of pressure and calculate the degree of dissociation of the gas at 100 c and 550c.
N2O4 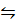 2NO2 (g)
2NO2 (g)
Start 1 0
Equilibrium: 1 2
2
But  = 50% = 0.5
= 50% = 0.5
1-0.5 2(0.5)
0.5 1
nT = 0.5 + 1
= 1.5 moles
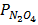 =
= 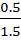 x 1
x 1  =
= 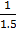 x 1
x 1
= 0.33 moles = 0.66moles
K p = 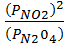
= 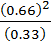
K p = 1.32
N2O4 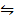 2NO2 (g)
2NO2 (g)
Start: 1 0
Equilibrium: 1-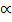 2
2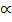
nT = (1- 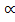 ) + 2
) + 2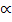
=1+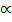
PT = 10atm
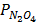 =
=  x 10
x 10  =
= 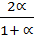 x 10
x 10
K p = 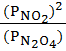
= 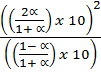
= 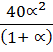 x 100 x
x 100 x 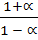 x
x 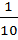
= 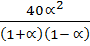
1.32 = 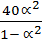
1.32 – 1.32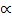 2 = 40
2 = 40 2
2
1.32 = 40 2 + 1.32
2 + 1.32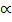 2
2
1.32 = 41.32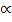 2
2
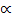 2 =0.0319
2 =0.0319
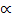 = 0.1787
= 0.1787
 Degree of dissociation = 17.87%
Degree of dissociation = 17.87%
DEGREE OF DISSOCIATION BY DENSITY MEASUREMENT
This method is used for the determination of degree of dissociation of gases in which 1 molecule produces 2 or more molecules.
i.e. PCl5 (g) 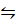 PCl3 (g) + Cl2 (g)
PCl3 (g) + Cl2 (g)
Thus at constant temperature and pressure, the volume increases. The density at constant pressure decreases.
The degree of dissociation can be calculated from the difference in density between the undissociated gas and that of partially dissociated gas at equilibrium.
If we start with 1 mole of the gas (PCl5) and the degree of dissociation (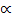 ), Then
), Then
PCl5 (g) 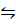 PCl3 (g) + Cl2 (g)
PCl3 (g) + Cl2 (g)
Moles at equilibrium: 1- 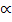
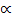
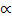
Total moles: 1 – 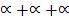
= 1+ 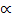
Note:
The density of an ideal gas at constant temperature and pressure is inversely proportional to the number of moles for a given weight.
Hence the ratio of density

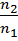
 =
= 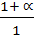
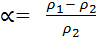 When
When 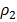 = Density of gas mixture of equilibrium
= Density of gas mixture of equilibrium
 = Density of gas before dissociation
= Density of gas before dissociation
 Degree of dissociation
Degree of dissociation
Examples1. When PCl5 is heated, it gasifies and dissociates into PCl3 and Cl2.The density of the gas mixture at 2000C is 70.2 Find the degree of dissociation of PCl5 at 2000C
Solution
Observed density, ρ2 =70.2
ρ1 =?
V.D = 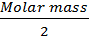
= 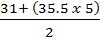
=104.25
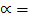
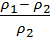
= 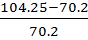
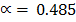
= 48.5%
2. At 900C, the V.D of N2O4 is 24.8. Calculate the % dissociation into NO2 molecules at this temperature.
N2O4  NO2 + NO2
NO2 + NO2
Density at equilibrium, ρ2 = 24.8
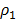 = V.D =
= V.D = 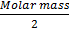 =
= 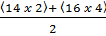 = 46
= 46
 ?
?
 =
= 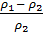
= 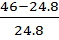
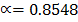
= 85.48%
DETERMINATION OF DEGREE OF DISSOCIATION BY MOLECULAR MASS
Molecular masses are proportional at constant temperature and pressure to the density of their gases; therefore we can substitute the molecular masses for the density in the degree of dissociation.
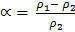

Where:-
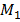 = Molecular mass of undissociated gas
= Molecular mass of undissociated gas
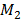 = Average Molecular mass of gases at equilibrium
= Average Molecular mass of gases at equilibrium
Example1:1.588g of N2O4 gives a total pressure of 1atm when partially dissociated at equilibrium in a 500cm3 glass vessel at 250C.What is the degree of dissociation at this temperature?
N2O4 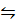 2NO2
2NO2
M1 = (14x 2) + (16 x4)
= 92gmol-1
M2 =?
From PV= nRT, W here n =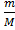
M2 = 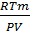
= 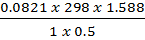
= 77.7gmol-1

= 
= 0.184
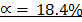
FACTORS AFFECTING EQUILIBRIUM REACTION
These factors are as follows:-
i) Temperature
ii) Concentration
iii) Pressure
The first three affects both rates and position of chemical equilibrium (i, ii and iii)
The other three affects the rate of chemical equilibrium
1) Temperature
a) Increasing the temperature, increases the rate of reaction because usually at high temperature the collision factor increases also the number
of molecules having necessary activation energy is large.
b) Effect on the position of equilibrium is explained by using Le-Chateliers principle which states that “when a system at equilibrium is
subjected to a change, processes occur which tend to counteract the change” (If a system in equilibrium is disturbed (change in temperature and pressure) the system adjusts itself so as to oppose the disturbance).
Consider the reaction
2SO2 (g) + O2 (g) 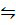 2SO3 (g) + Heat (negative)
2SO3 (g) + Heat (negative)
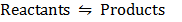
If temperature is increased in the system, the equilibrium moves in a direction where there is a absorption of heat and if the temperature is decreased in the system, the equilibrium moves in a direction where there is release of heat.
Effect of temperature, on the position of equilibrium can be explored by Vant Hoff`s law of
mobile chemical equilibrium which states that
“For any system in equilibrium high temperature favours endothermic reactions and low temperature favours exothermic reactions.
The way in which equilibrium constant changes with temperature is found both theoretically and experimentally governed by the following
relationship;
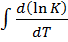 =
= 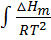
∆ Hm = change in molar heat
K = Equilibrium constant
On intergrating the equation above;

Where c = constant
If K1 and K2 are equilibrium constants corresponding to T1 and T2 ,the constant term can be eliminated from the equation above so as to give Vant Hoff`s equation i.e.
lnK1 = 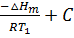 …………………. (1)
…………………. (1)
lnK2 = 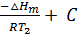 …………………. (2)
…………………. (2)
Subtracting equation (1) from (2) i.e.
lnK2 – lnK1 =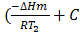 )
)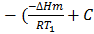 )
)
= 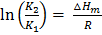
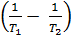 ……………………1
……………………1
But 1 ln = 2.303log
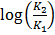 =
= 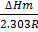
 ……………………2
……………………2
But  =
= 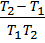
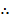
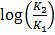 =
=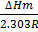
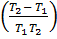 ……………………3
……………………3
Where 1 = 2 = 3
Example1: For the reaction;
N2O4 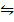 2NO2 ∆H = 61.5KJ mol-1
2NO2 ∆H = 61.5KJ mol-1
KP = 0.113 at 298K
i) What is the value of KP at 00C?
ii) At what temperature will KP =1?
Answers:
i) From 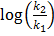 =
= 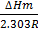
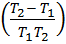
KP2 = 0.113
KP1 =?
T 1 = 273K
T 2 = 298K
∆Hm = 61.5Kjmol-1
R=8.314
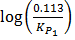 =
= 

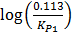 = 3211.9676 (3.0729896 x 10-4)
= 3211.9676 (3.0729896 x 10-4)
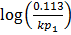 = 0.987
= 0.987
To remove ‘log’ make 100.987
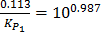
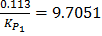
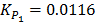
ii) From log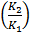 =
=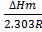
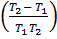
KP2 = 0.113 T1 =?
KP1 = 1 T2=298K
∆Hm = 61.5KJ mol-1
R = 8.314
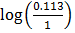 =
=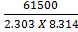
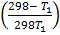
-0.9469 = 3211.9676 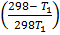
-2.948 x 10-4 = 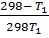
-0.0878T 1 = 298 – T 1
-0.0878T 1 + T1 =298
0.912T1 = 298
T1 = 326.7k