Form 5 Chemistry – PHYSICAL CHEMISTRY – Two Components Liquid System

 IMMISCIBLE LIQUIDS
Immiscible liquids are liquids which do not mix up to form homogeneous mixture.

When there are two immiscible liquids they form a so called immiscible pair.

Immiscible liquids form heterogeneous mixture.

For the immiscible liquids, the intermolecular force of attraction is greater compared to intermolecular forces of attraction , that’s why the liquids don’t mix up.

Since the liquids do not mix up, than their total vapor pressure (P_T) is equal to the sum of the pure vapor pressure of the components.

In immiscible liquids normally the denser component is found at the bottom (lower layer) while the less denser component is floating on the denser component (upper layer).

Example

Consider the immiscible pair of components A and B in which A denser than B

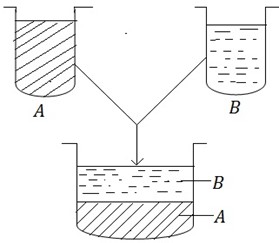
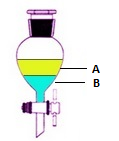
The immiscible pair is kept in a separating funnel in order to see them clearly.

Partition law states that

“When a solute that is soluble in both liquids is added, then it will dissolve”

The ration of concentration of solute added in a pair of a immiscible liquid is constant

i.e

The nglish-swahili/distribution” target=”_blank”>distribution of solute in a pair of immiscible liquid is governed by the Partition law or Distribution law.

PARTITION LAW

Partition law state that;

“In a pair of immiscible liquid, when solute which is soluble in both is added, it will distribute itself in such a way that the ratio of its concentration between the two liquid is constant.”

The constant in nglish-swahili/distribution” target=”_blank”>distribution law is termed as Distribution coefficient, Distribution constant or Partition constant. It is denoted by Kd or K_D.

Note

The solute added in a pair of immiscible mixture can be in either of three states (liquid, gases, solid).

APPLICATION OF PARTITION LAW

One of the application is the extraction of solute from one component by mixing the solution with the second liquid that has no solute at all.

The liquid component which is removing the solute is called Extracting component and that in which the solute is removed from is called Extracted component.

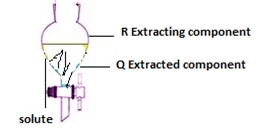
In terms of Extractions

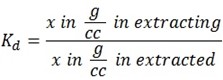
Note

Concentration is the amount of substance per unit volume.

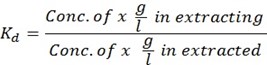
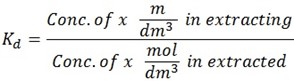
Also

NOTE

During extraction of solute the amount of solute in extracted component will be decreasing while the amount of extracting component will be increasing.

Example 1

a) State the partition law

Partition law state that;

“When a soluble solute is added in a pair of immiscible liquids, it will distribute itself in such a way that the ratio of its nglish-swahili/distribution” target=”_blank”>distribution between the two liquids is constant.”

b) What does the terms “Partition coefficient” mean?
Partition coefficient is the concentration of solute in immiscible liquids.

c) An aqueous solution containing 10g per litre of solute X. This solution was shake with 100cc of ether, on shaking 6g of X was extracted. Calculate the amount of X extracted from aqueous so residue after shaking with 100cc of ether.

Solution

Given

Extracted component = 10g/ l

Volume of extracting component = 100cc

Mass of X in water (aqueous solution) = 10g

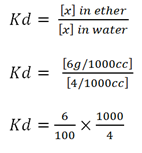
Kd = 15

Let the amount extracted be ‘a’

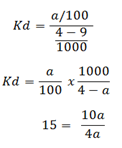
60 – 15a = 10a

60 = 10a + 15a

60 = 25a

a = 60/25

a = 2. 4g/cc

∴  The amount of X extracted from the aqueous residue is 2. 4g/cc.

NOTE

If layers are not specified then the word “between” shows the numerator and denominator of the formula.

Example 2

A solid X is added to a mixture of benzene and water after shaking well and allowing to hand, 10ml of benzene layer was found to certain 0. 13g of X and 100ml of water layer contained 0.22g of X.

Calculate volume of nglish-swahili/distribution” target=”_blank”>distribution coefficient of solute X between benzene and water layer

Solution

Mass of solute X in benzene = 0.13g

Volume of benzene = 10ml

Example3

In the nglish-swahili/distribution” target=”_blank”>distribution of succinic acid between ether and water at 15^oC , 20ml of the ethereal layer contains 0.092g of the acid. Find out the weight of the acid present in 50ml of the aqueous solution in equilibrium with it. If the coefficient kb between water and ether is (1.196g) and kd is 5.2

Solution

Mass of succinic acid in ethereal = 0.092g

Volume of ethereal = 20ml

Conc. Of succinic acid in ethereal = 0.092/20

= 4. 6 X 10^-3 g/mol

Coefficient of succinic acid between water and ethereal

= 5.2

Volume of water = 50ml

Let X be the weight of succinic acid in water

Conc. of succinic in water = W/50

From;

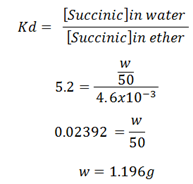
∴ The weight of the acid represent in aqueous solution 1.196g

Example 4

An aqueous solution of succinic acid at 15^oC containing 0.07g in 10ml is in equilibrium with an ethereal solution which has 0.013g in mo. The acid has its normal molecular weight in both solvents. What is the concentration of the ethereal solution which is in equilibrium with aqueous solution containing 0.024g in 1oml?
(Ans: 0.00044g/ml)

Solution

Mass of succinic acid in aqueous solution = 0.07g

Volume of aqueous solution = 10mls

Concentration of succinic in ethereal = 0.013

Concentration of succinic in solution = 0.07/10

= 7 X 10^-3

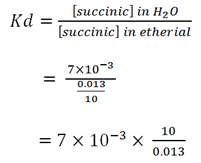
Kd = 5.38

Now

For second extraction

Mass of Aqueous solution = 0.024g

Volume of Aqueous solution  = 10ml

Conc. Of succinic in aqueous solution = 0.024/10

= 2.4 X 10^-3

Volume of ethereal = 10ml

Let X be the concentration of succinic acid in ethereal

For more than one extraction we normally use the following formula;

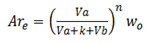
Where by;

Ar_e  is the amount of solute remain

Va is the volume of extracted solution

V_b is the volume of extracting solution

K is the constant of nglish-swahili/distribution” target=”_blank”>distribution

W_o is the original weight of the solute

From the formula, the amount extracted can be calculated as ( A ex)

A_ex = W_o
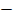Ar_e

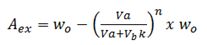
If the amount extracted and amount remained are known, then their respective percentages can be calculated.
i.e

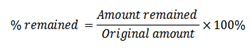
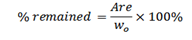
For extracted %

Example 1

Solute the partition law

Calculate the amount of solute extracted by shaking 1 litre of aqueous solution containing 11g of Q with;

i) 100ml of ether ( 10g)

ii) Two successive volume of 50ml of ether (kd = 100 ) ( 10. 69g )

Answer

The partition law states that;

“When a soluble solute is added in a pair of immiscible liquid, it will distribute itself in such a way that, the ration of its nglish-swahili/distribution” target=”_blank”>distribution in the liquid is constant”

Data given

Mass of solute Q = 11g

Volume of aqueous solution = 1 litre = 1000cc

Conc. Of Q in aqueous solution

Let X be the amount extracted

10x = 1100 – 100x

110x = 1100

x = 10g.

∴ The solute extracted is 10g.

b) (ii) Number of extraction = 2

volume of ether ( Vb ) = 50ml.

volume of water ( Vb ) = 1000ml.

kd = 100

Wo = 11g

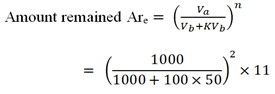
= 0.30556

Again

Aex = Wo – Are

= 11 – 0.3556

= 10.69g

∴  The solute extracted is 10.69g.

Example 2

a) Explain the principle of solvent extractions.

b) What is the condition necessary for solvent extraction?

Answer
b) The conditions of solvent extraction;
(i) The liquid to be mix must form immiscible solution.
(ii) the solute that is added to the extracted component  must be soluble to the extracting component like wise.

a) The principles of solvent extraction;

i) Division of the volume of extracting components

So as the extraction to be efficient the extracting components can be divided into two or more partitions.

ii) When a liquid A ( extracting component ) mixed with liquid B ( extracted component) must form the immiscible liquid with layer between them.

iii) The solute should be soluble in both liquid component hence it will allow its nglish-swahili/distribution” target=”_blank”>distribution such pair of immiscible liquid.

Example 3

a) State the partition law

Two form five girls each were given a solution which contains 10g of solute A in 900cc of solvent C. The first girl used 900cc of solvent B to extract solute from C. The second girl decided to use 300cc of B for the three extractions.

The nglish-swahili/distribution” target=”_blank”>distribution coefficient of solute A between C and B is 8.

i) Calculate the percentage of A left in C by the first girl.

ii) Calculate the percentage of A left in C by the second girl.

iii) Comment on the result obtained by the two girls.

Solution

a) Partition law states that:

“When a soluble solute is added in a pair immiscible liquid it will distribute itself in such a way that, the ratio of concentration of it in each component is constant”.

b) Solution

Mass of solute Wo = 10g

Volume of extracted = 900cc

Volume of extracting Vb = 900cc

Distribution constant Kd = 8

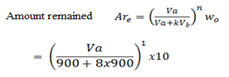
= 1.11g

% remained = 1.11/10 X 100 = 11%

ii) % remained by the second girl

= 2%

∴ The percentage of A left inn C by the second girl is 2%.

iii) For a successful extraction, the extracting liquid component must be divided into small portion as possible.

Example 4

Find out the principles of solvent extraction 100cm³ of there is available for extracting the solute X from 100cm³ of water. The partition coefficient of X between ether and water is 4.

i) Calculate the fraction of X extracted by using 100cm³ of ether all at once.

ii) Calculate the fraction of X extracted by using 4 ( If aqueous solution contains 8g of X )

Answer

The principles of solvent extraction.

i) The solute that is added in the immiscible mixture must be soluble to both liquids

So as the extraction to be perfect the extracting liquid must be divided into small portions as possible.

ii) When the extracted liquid is mixed with the extracting liquid, they should form immiscible mixture.

Solution

i) X extracted

given:

volume of extracting Vb = 100cm³

volume of extracted Va = 100cm³

Distribution constant k = 4

mass of solute X = 8g

from

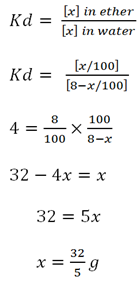
∴The fraction of X extraction is

ii) Fraction of X extracted by using two 50cm3

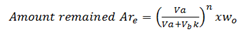
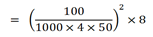
= 8/9

Amount extracted = 8 – 8/9

= 64/9 g

∴ The amount of X extracted by using 2, 50cm³ is  64/9 g.

Example 5.
The Mogul oil company is disturbed by the presence of impurity M In its for star petrol. 1 litre of petrol contains 5g of M. In an effort to decrease the concentration of M in a petrol, Mogul has discovered the secret of solvent S and the partition coefficient of M between petrol and S is 0.01.

a) What is meant by the term partition?

b) Explain the principle of solvent extraction

c) Calculate the total mass m of M removed in by using

i) One portion

ii) Two 50cm³ portion of solvent

Solution

a) Partition is the distribute of solvent in a pair of immiscible mixture.

b) i. The principle of solvent extraction;

“When the two components are added (extracted and extracting) they should form immiscible mixture.”

ii. The solute that is used must be soluble in both extracting and extracted component.

iii. The extracting component should be divided in small portions so as the experiment to be perfect.
c) Given

Volume of petrol Va = 1 litre = 1000cm³

Mass of M X = 5g

Distribution constant kd = 0.05

Volume of solvent S Vb = 100cc
i)

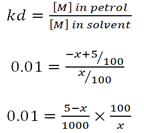
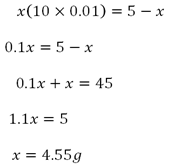
∴ The mass removed is 4.55g

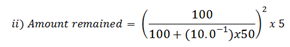
= 0.138g

∴ The amount removed is 5 – 0.138g = 4.86g.